Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ Path Length having Maximum Number of Bends
To solve a problem in which we are given a binary tree. Now we need to find the path having the maximum number of bends. i.e., A bend is considered when the direction of the path changes from left to right or vice versa, for example
Input −
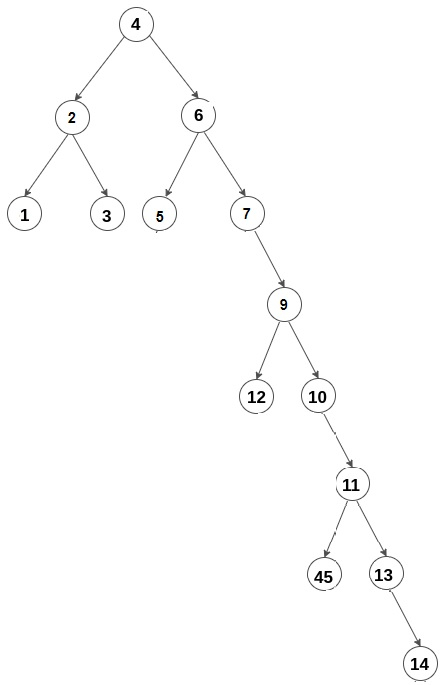
Output −
6
Now in this approach, we will traverse through the tree and keep track of previous movements. If the direction changes, we simply update our bends count, and then we find the maximum.
Approach to Find the Solution
In this approach, we will traverse through all the paths, and we find the maximum number of bends we update our answer.
Example
#include <bits/stdc++.h>
using namespace std;
struct Node { // structure of our node
int key;
struct Node* left;
struct Node* right;
};
struct Node* newNode(int key){ // initializing our node
struct Node* node = new Node();
node->left = NULL;
node->right = NULL;
node->key = key;
return node;
}
void maximumBends(struct Node* node,char direction, int bends,
int* maxBends, int soFar,int* len){
if (node == NULL) // if null is reached
return;
if (node->left == NULL && node->right == NULL) { // if we reach the leaf node then
//we check if we have to update our answer or not
if (bends > *maxBends) {
*maxBends = bends;
*len = soFar;
}
}
else {
if (direction == 'l') { // current direction is left
maximumBends(node->left, direction,bends, maxBends,soFar + 1, len);
maximumBends(node->right, 'r',bends + 1, maxBends,soFar + 1, len); // if we change direction so bend also increases
}
else {
maximumBends(node->right, direction,bends, maxBends,soFar + 1, len);
maximumBends(node->left, 'l',bends + 1, maxBends,soFar + 1, len); // same as when direction was left
}
}
}
int main(){
struct Node* root = newNode(10);
root->left = newNode(8);
root->right = newNode(2);
root->left->left = newNode(3);
root->left->right = newNode(5);
root->right->left = newNode(2);
root->right->left->right = newNode(1);
root->right->left->right->left = newNode(9);
int len = 0, bends = 0, maxBends = -1;
if(!root) // if tree is empty
cout << "0\n";
else{
if (root->left) // if left subtree exists
maximumBends(root->left, 'l',bends, &maxBends, 1, &len);
if (root->right) // if right subtree exists
maximumBends(root->right, 'r', bends,&maxBends, 1, &len);
cout << len << "\n";
}
return 0;
}Output
4
Explanation of the Above Code
In the above approach, we are simply traversing to all the paths and count the bend found so far now when we reach the end of the path .i.e leaf node, we check if the bends till here are greater than the previous maximum now if the condition is true, so we update our maximum bends and also the length of the path to this new length, and that’s how our program proceeds.
Conclusion
In this tutorial, we solve a problem to find the Path length having a maximum number of bends. We also learned the C++ program for this problem and the complete approach (Normal) by which we solved this problem. We can write the same program in other languages such as C, java, python, and other languages. We hope you find this tutorial helpful.
112 Views
To Continue Learning Please Login