
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Count the nodes whose sum with X is a Fibonacci number in C++
Given a binary tree with weights of its nodes as numbers. The goal is to find the number of nodes that have weights such that the number is a Fibonacci number. Numbers in Fibonacci series are: 0, 1, 1, 2, 3, 5, 8, 13….nth number is the sum of (n−1)th and (n−2)th. If weight is 13 then it is a Fibonacci number so the node will be counted.
For Example
Input
temp =1. The tree which will be created after inputting the values is given below −
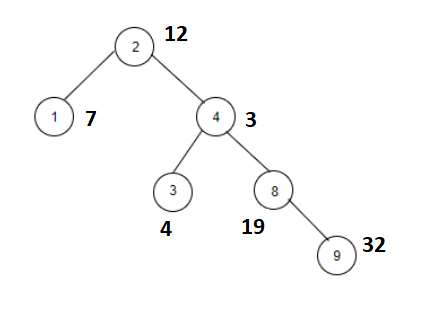
Output
Count the nodes whose sum with X is a Fibonacci number are: 3
Explanation
we are given with the tree nodes and the weights associated with each node. Now we check whether the temp+weight is a Fibonacci number or not.
| Node | Weight | Weight+temp=fibonacci | Yes/No |
|---|---|---|---|
| 2 | 12 | 12+1=13 | yes |
| 1 | 7 | 7+1=8 | yes |
| 4 | 3 | 3+1=4 | no |
| 3 | 4 | 4+1=5 | yes |
| 8 | 19 | 19+1=20 | no |
| 9 | 32 | 32+1=33 | no |
Input
temp = 3. The tree which will be created after inputting the values is given below −
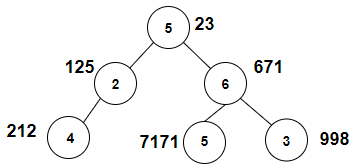
Output
Count the nodes whose sum with X is a Fibonacci number are: 3
Explanation
we are given with the tree nodes and the weights associated with each node. Now we check whether the temp+weight is a Fibonacci number or not.
| Node | Weight | Weight+temp=fibonacci | Yes/No |
|---|---|---|---|
| 5 | 23 | 23+3=26 | no |
| 2 | 125 | 125+3=128 | no |
| 6 | 671 | 671+3=674 | no |
| 4 | 212 | 212+3=215 | no |
| 5 | 7171 | 7171+3=7174 | no |
| 3 | 998 | 998+3=1001 | no |
Approach used in the below program is as follows −
In this approach we will apply DFS on the graph of the tree to traverse it and check if the weights of the node and temp add upto a fibonacci number. Take two vectors Node_Weight(100) and edge_graph[100] for this purpose.
Initialize Node_Weight[] with the weights of nodes.
Create a tree using vector edge_graph.
Take a global variable Fibonacci and initialize it with 0. Take other global variable temp.
Function check_square(long double val) takes an integer and returns true if val is a perfect square.
Take val_1 = sqrt(val)
Now if(val_1 − floor(val_1) == 0) returns true then total is a perfect square, return true.
Return false otherwise.
Function check_Fibonacci(int num) takes a number and returns true if it is a fibonacci number.
Initialize fib with 5*num*num.
If check_square((fib + 4)) || check_square((fib − 4)) results true then return true.
Return false otherwise.
Function Fibonacci_number(int node, int root) returns count of nodes whose sum with X is a Fibonacci number.
If if(check_Fibonacci(Node_Weight[node] + temp)) returns true then increment Fibonacci.
Traverse tree in vector edge_graph[node] using for loop.
Call Fibonacci_number(it, node) for the next node in the vector.
At the end of all functions we will have a Fibonacci as the number of nodes with weights having sum with temp as a fibonacci number.
Example
#include <bits/stdc++.h>
using namespace std;
vector<int> Node_Weight(100);
vector<int> edge_graph[100];
int Fibonacci = 0, temp;
bool check_square(long double val){
long double val_1 = sqrt(val);
if(val_1 − floor(val_1) == 0){
return true;
}
return false;
}
bool check_Fibonacci(int num){
int fib = 5 * num * num;
if(check_square((fib + 4)) || check_square((fib − 4))){
return true;
}
return false;
}
void Fibonacci_number(int node, int root){
if(check_Fibonacci(Node_Weight[node] + temp)){
Fibonacci++;
}
for (int it : edge_graph[node]){
if(it == root){
continue;
}
Fibonacci_number(it, node);
}
}
int main(){
//weight of the nodes
Node_Weight[2] = 6;
Node_Weight[1] = 4;
Node_Weight[4] = 23;
Node_Weight[3] = 5;
Node_Weight[8] = 161;
Node_Weight[9] = 434;
//create graph edge
edge_graph[2].push_back(1);
edge_graph[2].push_back(4);
edge_graph[4].push_back(3);
edge_graph[4].push_back(8);
edge_graph[8].push_back(9);
temp = 3;
Fibonacci_number(2, 2);
cout<<"Count the nodes whose sum with X is a Fibonacci number are: "<<Fibonacci;
return 0;
}
Output
If we run the above code it will generate the following output −
Count the nodes whose sum with X is a Fibonacci number are: 1

