Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Count full nodes in a Binary tree (Iterative and Recursive) in C++
We are given a binary tree and the task is to calculate the count of full nodes available in a binary tree using iterative and recursive approach. Full nodes are those nodes who have both the children and no child is null. Note that in full nodes we consider nodes with exactly two children.
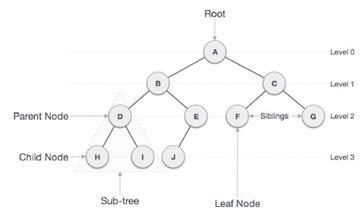
Binary Tree is a special data structure used for data storage purposes. A binary tree has a special condition that each node can have a maximum of two children. A binary tree has the benefits of both an ordered array and a linked list as search is as quick as in a sorted array and insertion or deletion operation are as fast as in linked list. Non-leaf nodes are also known as parent nodes as they have more than 0 child and less than two children.
Structure of a binary tree is given below −
For Example
Input−
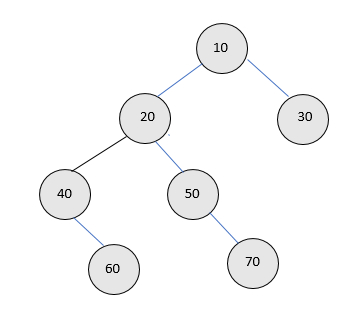
Output − count is 2
Explanation − in the given tree there are 2 nodes i.e. 10 and 20 with exactly two children or full nodes other nodes either have one child or no child.
Iterative
Approach used in the below program is as follows
Create a structure of a node containing a data part, left pointer and right pointer.
Create a function to insert the nodes in a binary tree.
Create a function to count the full nodes.
Inside a function, check IF !node then return as there is no node in a tree.
Declare a temporary variable count to store the count of full nodes
Create a queue type variable let’s say qu
Push the nodes in a queue as qu.push(node)
Loop while !qu.empty()
Create a temporary variable let’s say temp of Node type and initialize it with queue.front()
Pop the elements using qu.pop()
Check IF (!temp-> left AND temp-> right) then increment the count by 1
Check IF (temp->left != NULL) then perform qu.push(temp->left)
Check IF (temp->right != NULL) then qu.push(temp->right)
Return the count
Print the result.
Example
// Iterative program to count full nodes
#include <iostream>
#include <queue>
using namespace std;
struct Node{
int data;
struct Node* left, *right;
};
// Function to count the full Nodes in a binary tree
int fullcount(struct Node* node){
// Check if tree is empty
if (!node){
return 0;
}
queue<Node *> myqueue;
// traverse using level order traversing
int result = 0;
myqueue.push(node);
while (!myqueue.empty()){
struct Node *temp = myqueue.front();
myqueue.pop();
if (temp->left && temp->right){
result++;
}
if (temp->left != NULL){
myqueue.push(temp->left);
}
if (temp->right != NULL){
myqueue.push(temp->right);
}
}
return result;
}
struct Node* newNode(int data){
struct Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return (node);
}
int main(void){
struct Node *root = newNode(10);
root->left = newNode(20);
root->right = newNode(30);
root->left->left = newNode(40);
root->left->right = newNode(50);
root->left->left->right = newNode(60);
root->left->right->right = newNode(70);
cout <<"count is: "<<fullcount(root);
return 0;
}Output
If we run the above code we will get the following output −
count is: 2
Recursive
Approach used in the below program is as follows
Create a structure of a node containing a data part, left pointer and right pointer.
Create a function to insert the nodes in a binary tree.
Create a function to count the full nodes.
Inside a function, check IF !node then return as there is no node in a tree.
Declare a temporary variable count to store the count of half nodes
Check IF (root -> left AND root->right) then increment the count by 1
Set count = count + recursive_call_to_this_function(root->left) + recursive_call_to_this_function(root->right)
Return the count
Print the result.
Example
// Recursive program to count full nodes
#include <iostream>
using namespace std;
struct Node{
int data;
struct Node* left, *right;
};
// Function to get the count of full Nodes
int fullcount(struct Node* root){
if (root == NULL){
return 0;
}
int result = 0;
if (root->left && root->right){
result++;
}
result += (fullcount(root->left) +
fullcount(root->right));
return result;
}
struct Node* newNode(int data){
struct Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return (node);
}
int main(){
struct Node *root = newNode(10);
root->left = newNode(20);
root->right = newNode(30);
root->left->left = newNode(40);
root->left->right = newNode(50);
root->left->left->right = newNode(60);
root->left->right->right = newNode(70);
cout <<"count is: "<<fullcount(root);
return 0;
}Output
If we run the above code we will get the following output −
count is: 2
927 Views
