Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Container with Most Water in C++
We are given an array of height of the walls of the container. The goal is to find the container that can contain the maximum volume of water. As heights of walls are elements of an array, the distance between them is considered as width between two walls. For example walls of height Arr[i] and Arr[j] have j-i width between them ( 0<=i<j<=N), where N is no. of walls or length of the array.
So the height of water will be up to the lesser height, if Arr[i] < Arr[j] height of water will be Arr[i]. Width is j-i so area for water = Arr[i] * ( j- i ).
We have to find the maximum such area.
Input
Arr[]= { 5,1,2,3,5 }Output
Maximum water area : 20
Explanation
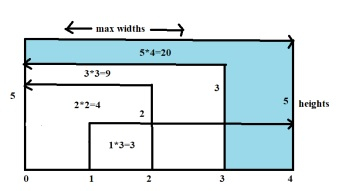
As shown in the figure, for wall heights 5,1,2,3 and maximum widths between walls are
Arr[0] and Arr[4] width=4, area = Arr[0]<=Arr[4] → 5*4=20 Arr[1] and Arr[4] width=3, area = Arr[1]<=Arr[4] → 1*4=4 Arr[2] and Arr[0] or Arr[4] width=4, area = Arr[0]<=Arr[0] → 2*2=4 Arr3] and Arr[0] width=3, area = Arr[0]<=Arr[0] → 3*3=9 Arr[4] and Arr[0] width=4, area = Arr[0]<=Arr[4] → 5*4=20
Maximum area container will have maximum water, area=20, walls Arr[0] and Arr[4]
Input
Arr[]= { 1, 5, 4, 3, 2, 4 }Output
Maximum water area : 16
Explanation
Arr[0] and Arr[5] width=5, area = Arr[0]<=Arr[5] → 1*5= 5 Arr[1] and Arr[5] width=4, area = Arr[1]<=Arr[5] → 4*4=16 Arr[2] and Arr[5] width=3, area = Arr[2]<=Arr[5] → 3*4=12 Arr[3] and Arr[1] width=2, area = Arr[3]<=Arr[1] → 3*2=6 Arr[4] and Arr[1] width=3, area = Arr[1]<=Arr[4] → 2*3=6 Arr[5] and Arr[1] width=4, area = Arr[1]<=Arr[4] → 4*4=16
Maximum area container will have maximum water, area=16, walls Arr[0] and Arr[4]
Approach used in the below program is as follows
The integer array walls[] contains heights of walls.
Function mostwater(int A[], int len) takes array of heights and the no. of elements in it and returns the area of container with most water as only height and width are available.
We take two indexes r=len-1 and l=0 to start traversing the array from both ends.
Integers area and maxarea are used to store area of current container and maximum container area found so far respectively. Initially 0
int minwall,lwall,rwall stores the height of left wall ( A[l] ), right wall ( A[r] ), and minimum height of lwall and rwall;
While ( l<r ) traverse array and for each A[l] and A[r], height of water will be minimum of two. Whichever is minimum store in minwall
Width between two walls is difference of indexes ( r-l )
Calculate area of water/container as minwall* ( r-l ) and update area.
Do this for all walls, if current area is maximum so far update maxarea.
In the end maxarea will have the desired area of container with most water.
- Return maxarea as result.
Example
#include<iostream>
using namespace std;
int mostwater(int A[], int len){
int r=len-1; //index of right wall of container
int l=0; //index of left wall of container
int area=0,maxarea=0;
int minwall,lwall,rwall;
// int area = 0;
while (l < r){
// Calculating the max area
lwall = A[l]; //height of left wall of container
rwall =A[r]; //height of right wall of container
minwall=lwall<=rwall?lwall:rwall; //min. of two walls is height of water
area=minwall*(r-l); // area is min wall* widht(r-l)
maxarea=area>=maxarea?area:maxarea;
if (l < r)
l += 1;
else
r -= 1;
}
return maxarea;
}
int main(){
int walls[] = {1, 5, 4, 3, 2, 4};
int num = sizeof(walls) / sizeof(walls[0]);
cout << endl <<"Container with Most water has area:"<< mostwater(walls,num);
}Output
Container with Most water has area:16
124 Views
