- Computer Security Tutorial
- Computer Security - Home
- Computer Security - Overview
- Computer Security - Elements
- Computer Security - Terminologies
- Computer Security - Layers
- Computer Security - Securing OS
- Computer Security - Antiviruses
- Computer Security - Malwares
- Computer Security - Encryption
- Computer Security - Data Backup
- Disaster Recovery
- Computer Security - Network
- Computer Security - Policies
- Computer Security - Checklist
- Legal Compliance
- Computer Security Useful Resources
- Computer Security - Quick Guide
- Computer Security - Resources
- Computer Security - Discussion
Computer Security - Malwares
In the previous chapter we treated antiviruses which helped us to protect our systems but in this chapter we will treat malwares, how to detect them manually, what are their forms, what are their file extensions, signs of an infected computer, etc. They are important to be treated because the infection rates of businesses and personal computers are too high in nowadays.
They are self-replication programs that reproduce their own codes by attaching themselves to other executable codes. They operate without the permissions or knowledge of the computer users. Viruses or malwares like in real-life, in computers they contaminate other healthy files.
However, we should remember that viruses infect outside machines only with the assistance of a computer user only. These can happen by clicking a file that comes attached with email from an unknown person, plugging a USB without scanning, opening unsafe URLs for that reason. We as system administrators have to remove the administrator permissions of users in these computers. We categorize malwares in three types −
- Trojans and Rootkits
- Viruses
- Worms
Characteristics of a Virus
Following are a couple of characteristics of any virus that infects our computers.
They reside in a computer’s memory and activates themselves while the program that is attached starts running.
For example − They attach themselves in general to the explorer.exe in windows OS because it is the process that is running all the time, so you should be cautious when this process starts to consume too much of your computer capacities.
They modify themselves after the infection phase like they source codes, extensions, new files, etc. so it is harder for an antivirus to detect them.
They always try to hide themselves in the operating systems in the following ways −
Encrypts itself into cryptic symbols, and they decrypt themselves when they replicate or execute.
For example − You can see this in the following image for better understanding as in my computer I found this file.
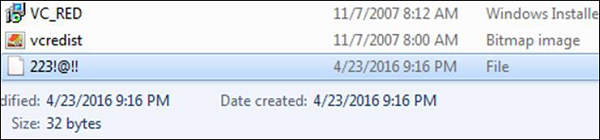
After finding this file, I opened it with a text editor and as thought the text was not understandable as shown in the following screenshot.
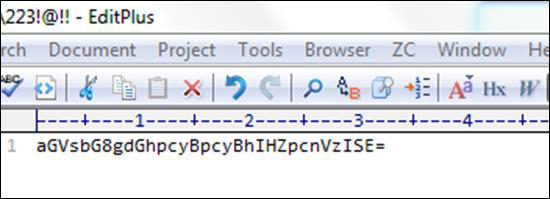
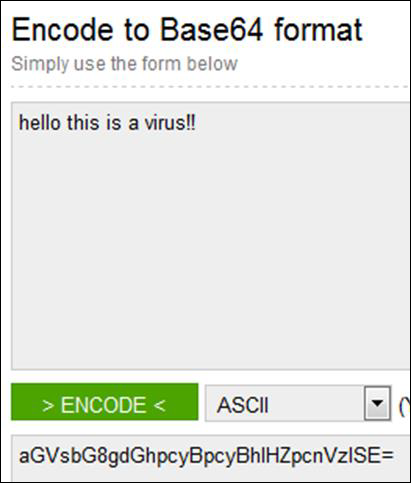
After finding this, I tried it on a base64 decoder and I found that it was a Virus file.
This virus can cause the following to your computer −
It may delete important data from your computer to gain space for their processes.
It may avoid detection by redirection of disk data.
It may perform tasks by triggering an event with itself. For example, this happens when in an infected computer pop-up tables etc., show up automatically on the screen.
They are common in Windows and Mac OS because these operation systems do not have multiple file permissions and are more spread out.
Working Process of Malwares and how to Clean it
Malwares attach themselves to programs and transmit to other programs by making use of some events, they need these events to happen because they cannot −
- Start by themselves
- Transmit themselves by using non-executable files
- Infect other networks or computer
From the above conclusions, we should know that when some unusual processes or services are run by themselves we should further investigate their relations with a possible virus. The investigation process is as follows −
To investigate these processes, start with the use of the following tools −
- fport.exe
- pslist.exe
- handle.exe
- netstat.exe
The Listdll.exe shows all the dll files being used, while the netstat.exe with its variables shows all the processes that are being run with their respective ports.
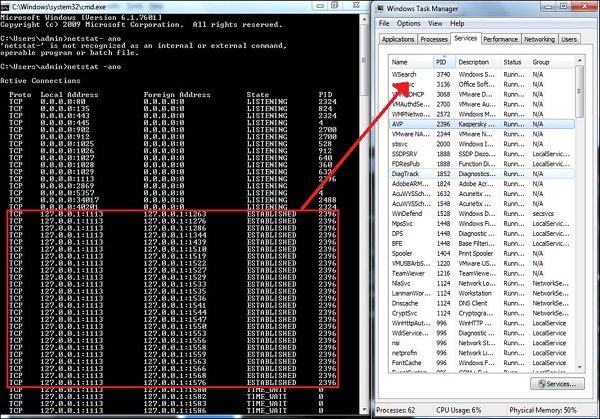
You can see the following example on how I mapped the process of Kaspersky antivirus which I used along with the command netstat-ano to see the process numbers and task manager to see to which process belongs to this number.
Then we should look for any modified, replaced or deleted files and the shared libraries should also be checked. They generally infect executable program files with extension like .EXE, .DRV, .SYS, .COM, .BIN. Malwares changes extension of genuine files, for example: File.TXT to File.TXT.VBS.
If you are a system administrator of a webserver, then you should be aware of another form of malware which is called as webshell. It generally is in a .php extension but with strange file names and in an encrypted form. You should delete them in case you detect them.
After that is done, we should update the antivirus program and rescan the computer again.
Detecting a Computer Error from a Virus Infection
In this section we will treat how to detect a computer or OS fault from a virus because sometimes people and system administrators mix the symptoms.
The following events are most likely not caused by a malware −
- Error while the system is booting in bios stage, like Bios’s battery cell display, timer error display.
- Hardware errors, like beeps RAM burn, HDD, etc.
- If a document fails to start normally like a corrupted file, but the other files can be opened accordingly.
- Keyboard or mouse doesn’t answer to your commands, you have to check the plug-ins.
- Monitor switching on and off too often, like blinking or vibrating, this is a hardware fault.
On the other hand, if you have the following signs in your system, you should check for malware.
Your computer shows a pop-up or error tables.
Freezes frequently.
It slows down when a program or process starts.
Third parties complain that they are receiving invitation in social media or via email by you.
Files extensions changes appear or files are added to your system without your consent.
Internet Explorer freezes too often even though your internet speed is very good.
Your hard disk is accessed most of the time as you can see from the LED light on your computer case.
OS files are either corrupted or missing.
If your computer is consuming too much bandwidth or network resources this is the case of a computer worm.
Hard disk space is occupied all the time, even when you are not taking any action, for example installing a new program.
Files and program sizes changes comparing to its original version.
Some Practical Recommendations to Avoid Viruses −
- Don’t open any email attachment coming from unknown people or from known people that contain suspicious text.
- Don’t accept invitation from unknown people on social media.
- Don’t open URL sent by unknown people or known people that are in any weird form.
Virus Information
If you have found a virus but you want to investigate further regarding its function. I would recommend you to have a look at these virus databases, which are offered generally by antivirus vendors.
Kaspersky Virus Database − (http://www.kaspersky.com/viruswatchlite?hour_offset=-1)
F-Secure − (https://www.f-secure.com/en/web/labs_global/threat-descriptions)
Symantec – Virus Encyclopedia − (https://www.symantec.com/security_response/landing/azlisting.jsp)