Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Binary Tree Representation in Data Structures
Here we will see how to represent a binary tree in computers memory. There are two different methods for representing. These are using array and using linked list.
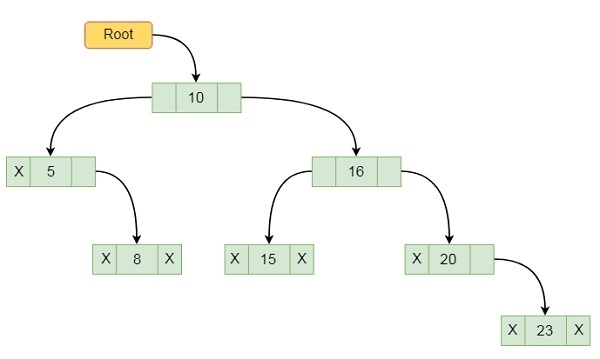
Suppose we have one tree like this −
The array representation stores the tree data by scanning elements using level order fashion. So it stores nodes level by level. If some element is missing, it left blank spaces for it. The representation of the above tree is like below −
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 10 | 5 | 16 | - | 8 | 15 | 20 | - | - | - | - | - | - | - | 23 |
The index 1 is holding the root, it has two children 5 and 16, they are placed at location 2 and 3. Some children are missing, so their place is left as blank.
In this representation we can easily get the position of two children of one node by using this formula −
$$child_{1}=2*parent$$
$$child_{2}=\lgroup2*parent\rgroup+1$$
To get parent index from child we have to follow this formula −
$$parent=\begin{bmatrix}\frac{child}{2} \end{bmatrix}$$
This approach is good, and easily we can find the index of parent and child, but it is not memory efficient. It will occupy many spaces that has no use. This representation is good for complete binary tree or full binary tree.
Another approach is by using linked lists. We create node for each element. This will be look like below −
13K+ Views
