Binary Tree Level Order Traversal in C++

Suppose we have a binary tree. We have to traverse this tree using the level order traversal scheme. So if the tree is like

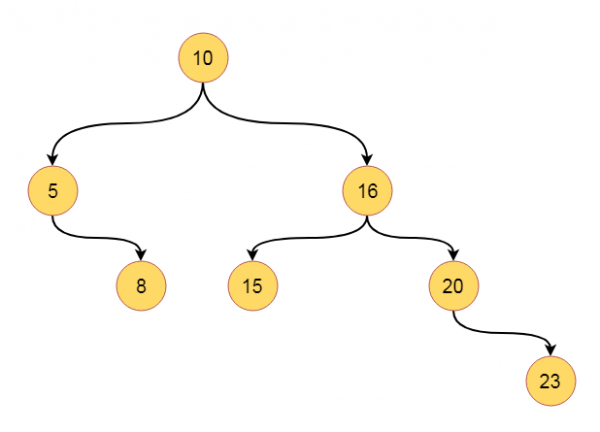
The traversal sequence will be like − [10, 5, 16, 8, 15, 20, 23]

To solve this, we will follow these steps −

• define queue que to store nodes
• insert root into the que.
• while que is not empty, do
  • item := item present at front position of queue
  • print the value of item
  • if left of the item is not null, then insert left of item into que
  • if right of the item is not null, then insert right of item into que
  • delete front element from que

Example(C++)

Let us see the following implementation to get a better understanding −

 Live Demo

#include<iostream>
#include<queue>
using namespace std;
class node{
   public:
      int h_left, h_right, bf, value;
      node *left, *right;
};
class tree{
   private:
      node *get_node(int key);
   public:
      node *root;
      tree(){
         root = NULL; //set root as NULL at the beginning
      }
      void levelorder_traversal(node *r);
      node *insert_node(node *root, int key);
};
node *tree::get_node(int key){
   node *new_node;
   new_node = new node; //create a new node dynamically
   new_node->h_left = 0; new_node->h_right = 0;
   new_node->bf = 0;
   new_node->value = key; //store the value from given key
   new_node->left = NULL; new_node->right = NULL;
   return new_node;
}
void tree::levelorder_traversal(node *root){
   queue <node*> que;
   node *item;
   que.push(root); //insert the root at first
   while(!que.empty()){
      item = que.front(); //get the element from the front end
      cout << item->value << " ";
      if(item->left != NULL) //When left child is present, insert into queue
         que.push(item->left);
      if(item->right != NULL) //When right child is present, insert into queue
         que.push(item->right);
      que.pop(); //remove the item from queue
   }
}
node *tree::insert_node(node *root, int key){
   if(root == NULL){
      return (get_node(key)); //when tree is empty, create a node as root
   }
   if(key < root->value){ //when key is smaller than root value, go to the left
      root->left = insert_node(root->left, key);
   }
   else if(key > root->value){ //when key is greater than root value, go to the right
      root->right = insert_node(root->right, key);
   }
   return root; //when key is already present, do not insert it again
}
main(){
   node *root;
   tree my_tree;
   //Insert some keys into the tree.
   my_tree.root = my_tree.insert_node(my_tree.root, 10);
   my_tree.root = my_tree.insert_node(my_tree.root, 5);
   my_tree.root = my_tree.insert_node(my_tree.root, 16);
   my_tree.root = my_tree.insert_node(my_tree.root, 20);
   my_tree.root = my_tree.insert_node(my_tree.root, 15);
   my_tree.root = my_tree.insert_node(my_tree.root, 8);
   my_tree.root = my_tree.insert_node(my_tree.root, 23);
   cout << "Level-Order Traversal: ";
   my_tree.levelorder_traversal(my_tree.root);
}

Input

[10,5,16,null,8,15,20,null,null,null,null,null,null,null,23]

Output

Level-Order Traversal: 10 5 16 8 15 20 23