Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
In-order traversal in Javascript Tree
The tree is a data structure that is comprised of nodes and edges. These entities are interconnected to each other to form a tree structure.
Traversing a data structure means visiting each and every node in that structure and bringing out a sequence of values from that. There are three types of traversals namely, in-order (L→ Root→R ), pre-order(Root→L→R) and, post-order(L→ R → Root)
In-order Traversal
In the In-order Traversal, the left subtree is visited first, followed by the Root node and finally the right subtree. A binary tree will provide sorted key values in ascending order if it is traversed in-order.
It will represent as
LEFT → ROOT → RIGHT
Consider the following binary search tree,
The traversal starts from the root node A, and checks whether the root node A has a left subtree. As it exists, it moves to the left subtree, B. There is no subtree present after B, A (Root node) will be traversed and goes to the right subtree C to check if it has a left subtree. This process will go on until all nodes are traversed.
The output of the above Inorder tree traversal will be −
B → A → D → C → F → E → G
Algorithm
In order (Tree)
Traverse the left subtree, leftmost node in the tree will be printed first (LeftSubtree).
Goes back to the Root, the root is printed.
Traverse the right subtree, rightmost node will be printed last (Right-Subtree).
Binary search tree with added nodes
Consider a new scenario where there are more nodes inserted in the tree.
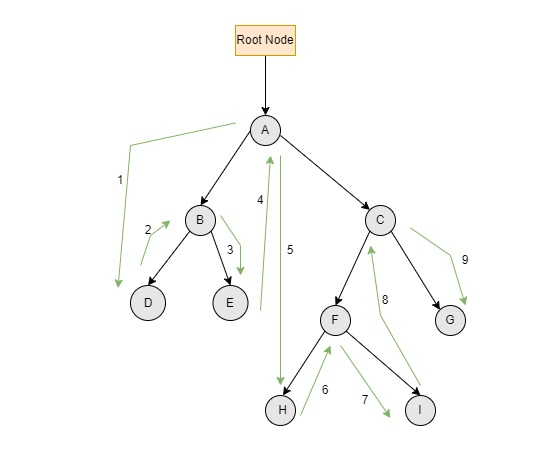
The green arrows in the above figure indicate the direction of the inorder traversal.
The end results of the presented binary tree are as follows: D→ B→ E→ A→ H→ F→ I→ C→ G
Example 1 (Using Recursion)
The following code provides a description of the in order tree traversal with recursion technique.
<!DOCTYPE html> <html> <head> <script> class Node { constructor(value) { this.key = value; this.left = null; this.right = null; } } var root = null; function TreeInorder(node) { if (node == null) return; TreeInorder(node.left); document.write(node.key + "→"); TreeInorder(node.right); } root = new Node('A'); root.left = new Node('B'); root.right = new Node('C'); root.right.left = new Node('D'); root.right.right = new Node('E'); root.right.right.left = new Node('F'); root.right.right.right = new Node('G'); document.write("<br/>Inorder traversal of the tree is<br/>"); TreeInorder(root); </script> </head> </html>
Output
The output of the above script will be −
Inorder traversal of the tree is
B → A → D → C → F → E → G →
Example 2 (Using Stack)
Another way to traverse tree in in-order technique can be done using stack.
<!DOCTYPE html> <html> <head> <script> class Node { constructor(stack) { this.data = stack; this.left = this.right = null; } } var root_Node; function inorderUsingStack() { if (root_Node == null) return; let stack = []; let current_Node = root_Node; while (current_Node != null || stack.length > 0) { while (current_Node != null) { stack.push(current_Node); current_Node = current_Node.left; } current_Node = stack.pop(); document.write(current_Node.data + "→"); current_Node = current_Node.right; } } root_Node = new Node('A'); root_Node.left = new Node('B'); root_Node.right = new Node('C'); root_Node.right.left = new Node('D'); root_Node.right.right = new Node('E'); root_Node.right.right.left = new Node('F'); root_Node.right.right.right = new Node('G'); inorderUsingStack(); </script> </head> </html>
Output
The output of the above script will be −
B → A → D → C → F → E → G →
2K+ Views
