
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Print level order traversal line by line in C++ Programming.
Level Order Traversal, also known as Breadth-First Search (BFS), is a method of traversing a tree where nodes are visited level by level, starting from the root node and moving left to right within each level.
In this article, our task is to print the nodes of a binary tree in level order, with each level displayed on a separate line. For example, if the binary tree (consider the below image) is traversed in level order.
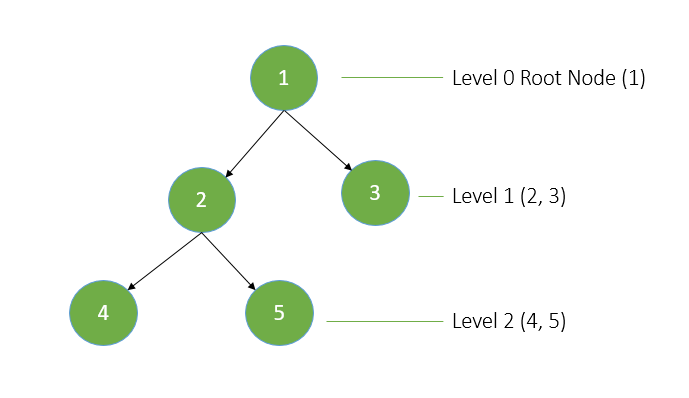
The output will look like this:
1 2 3 4 5
Printing Level Order Traversal Line by Line
The following are the Approaches to print level order traversal line by line of a binary tree. Let's see how we implement it in C++:
- Using Recursion
- Using BFS with a Queue
Using Recursion
A recursion is a programming technique where a function calls itself either directly or indirectly.
To traverse a binary tree in level-order and print each level on a new line, we can use a recursive approach that divides the problem into smaller subproblems. In this method, the recursive function is designed to handle one level at a time, calling itself for the next level, allowing the tree to be processed level by level.
Algorithm
The following are the steps to implement recursively:
- First, we start with root node at level 0
- Create a result array to store nodes level-by-level
- Traverse the tree recursively, passing the current node and its level as parameters.
- At each node, if the current level does not exist in the result array, create a new list for that level.
- Add the value of the node to the list at the index equal to the current level.
- Visit the left and right children, increasing the level by 1 for each call, recursively.
Example
In the following C++ example, we perform the level order traversal using recursion:
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node *left, *right;
// Constructor to initialize a new node
Node(int value) {
data = value;
left = nullptr;
right = nullptr;
}
};
void levelOrderRec(Node* root, int level, vector<vector<int>>& res) {
// Base case: If node is null, return
if (root == nullptr)
return;
// Add a new level to the result if needed
if (res.size() <= level)
res.push_back({});
// Add current node's data to its corresponding level
res[level].push_back(root->data);
// Recur for left and right children
levelOrderRec(root->left, level + 1, res);
levelOrderRec(root->right, level + 1, res);
}
// Function to perform level order traversal
vector<vector<int>> levelOrder(Node* root) {
vector<vector<int>> res;
levelOrderRec(root, 0, res);
return res;
}
int main() {
Node* root = new Node(5);
root->left = new Node(6);
root->right = new Node(7);
root->left->left = new Node(8);
root->left->right = new Node(9);
root->right->left = new Node(10);
root->right->right = new Node(11);
vector<vector<int>> res = levelOrder(root);
cout<<"Level Order Traversal:"<<'\n';
for (vector<int> level : res) {
for (int i = 0; i < level.size(); i++) {
cout << level[i];
if (i < level.size() - 1) cout << ", ";
}
cout<<"\n";
}
return 0;
}
Following is the output of the above code:
Level Order Traversal: 5 6, 7 8, 9, 10, 11
Using BFS with a Queue
In this approach, we use level-order traversal with BFS by using the queue to traverse nodes level-by-level. It displays each level's node of the binary tree on a new line and processes nodes from left to right at each level.
Algorithm
- Start from the root node of the binary tree.
- Check if the tree is empty (i.e., root is NULL): If yes then return.
- Create an empty queue and push the root node into it.
- Repeat the below steps while the queue is not empty:
- Get the number of nodes at the current level using
queue.size(). - Use a loop to process all nodes at the current level (while count > 0):
- Get the front node from the queue and print its data.
- Remove (pop) the front node from the queue.
- If the node has a left child, push it into the queue.
- If the node has a right child, push it into the queue.
- Decrease the count by 1.
- After finishing one level, move to the next line (print
\n) to show separation between levels. - Continue this process until all nodes in the tree are printed level-by-level.
Example
In the following example, we perform level order traversal using BFS with a queue to print each node in a new line for every level:
#include <iostream>
#include <queue>
using namespace std;
//it will create a node structure
struct node{
struct node *left;
int data;
struct node *right;
};
void levelorder(node *root){
if (root == NULL)
return;
queue<node *> que;
que.push(root);
cout<<"Level order traveral"<<"\n";
while (que.empty() == false){
int count = que.size();
while (count > 0){
node *node = que.front();
cout << node->data << " ";
que.pop();
if (node->left != NULL)
que.push(node->left);
if (node->right != NULL)
que.push(node->right);
count--;
}
cout<<"\n";
}
}
//it will create a new node
node* newnode(int data){
node *temp = new node;
temp->data = data;
temp->left = NULL;
temp->right = NULL;
return temp;
}
int main(){
// it will generate the binary tree
node *root = newnode(1);
root->left = newnode(2);
root->right = newnode(3);
root->left->left = newnode(4);
root->left->right = newnode(5);
levelorder(root);
return 0;
}
Following is the output of the above code:
Level order traveral 1 2 3 4 5
Conclusion
A level-order traversal is a BFS that takes O(n) time complexity in a binary tree. We use a level-order traversal to print all nodes of a binary tree level by level.

