Basic Proportionality Theorem & Similar Triangles

Introduction

Basic proportionality theorem was proposed by a famous Greek mathematician, Thales, hence, it is also referred to as the Thales theorem. Triangle is one of the basic geometrical shapes with three sides & three angles. In geometry you have studied different properties & theorems of the triangle. In this tutorial, we will study one of the most important properties i.e., similarity & basic proportionality theorem. Two triangles are said to be similar if their angles are congruent & corresponding sides are in proportion. '$\mathrm{\sim}$' symbol is used to represent similar triangles. There are several methods for finding whether triangles are similar or not. It is based on the property of the similarity of triangle.

Similarity of triangle

Any two geometrical figures are said to be similar if they have the same shape, not necessarily the same size. When similar shapes magnifies or demagnifies superimpose each other. They superimpose each other when they are placed at different orientation.

If two triangles are said to be similar if their angles are equal & their corresponding sides are in proportion. '$\mathrm{\sim}$' symbol is used to represent similar triangles.

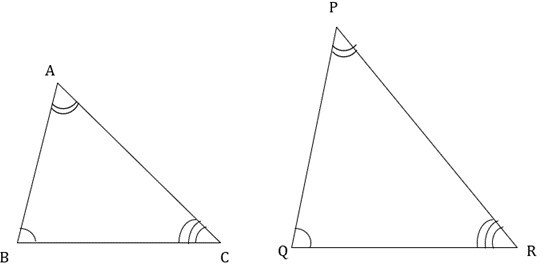
In the above figure,

If $\mathrm{\angle A \cong \angle P}$

$\mathrm{\angle B \cong \angle Q}$

$\mathrm{\angle C \cong \angle R}$

Also,$\mathrm{\frac{AB}{PQ}=\frac{BC}{QR}=\frac{AC}{PR}}$

From above, the angles of two triangles are equal & sides are in proportion.

Therefore, △ ABC & △ PQR are similar triangles.

Mathematically it can be expressed as, △ ABC ∼ △ PQR.

Some properties of similar triangles

Reflexivity

Every triangle is similar to itself. For example, △ ABC ∼ △ ABC

Symmetry

If △ ABC ∼ △ PQR then △ PQR ∼ △ ABC

Transitivity

If △ ABC ∼ △ PQR & △ PQR ∼ △ XYZ then △ ABC ∼ △ XYZ

Similarity criterion

• By using the similarity criterion, we can prove whether triangles are similar or not.

• There are three criteria for checking the similarity of the triangle. They are as follows −

  • AAA criteria

  • SSS criteria

  • SAS criteria

AAA criteria

• In two triangles if the corresponding angles are equal, then their corresponding sides are in proportion.

• This criterion is known as AAA (angle-angle-angle) criteria of two similar triangles.

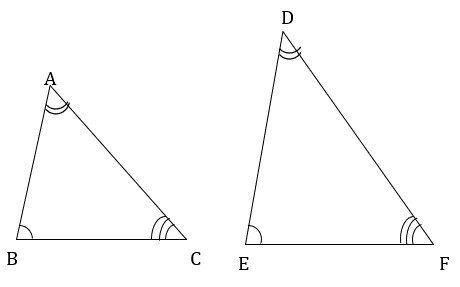
In △ ABC & △ DEF, in correspondence ABC ↔ PQR

$$\mathrm{\angle A \cong \angle D}$$

$$\mathrm{\angle B \cong \angle E}$$

$$\mathrm{\angle C \cong \angle F}$$

Given triangles satisfies AAA criteria.

Therefore, △ ABC ∼ △ DEF.

If two angles of one triangle are congruent to two corresponding angles of another triangle, then the two triangles are similar. This is known as AA criteria of similartiy of two triangles.

SSS criteria

• In two triangles, if the sides of one triangle are proportional to the sides of other triangles, then their corresponding angles are equal the two triangles are similar.

• This is known as SSS (side-side-side) criteria of similar triangles.

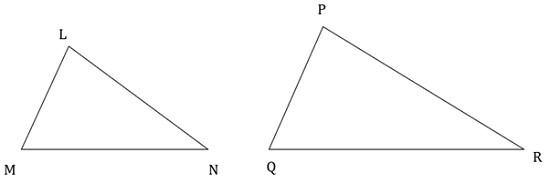
In △ LMN & △ PQR

$$\mathrm{\frac{LM}{PQ}=\frac{MN}{QR}=\frac{LN}{PR}}$$

Given triangles satisfies SSS criteria

Therefore, △ LMN ∼ △ PQR

SAS criteria

• In two triangles, if one angle of a triangle is equal to one angle of another triangle & sides, including the angle are proportional, then the two triangles are similar.

• This is known as SAS (side-angle-side) criteria for similarity of two triangles.

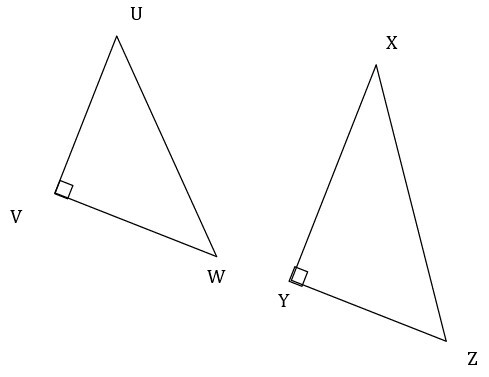
In △ UVW & △ XYZ

If $\mathrm{\angle V \cong \angle Y}$

Also, $\mathrm{\frac{UV}{XY}=\frac{VW}{YZ}}$

Therefore, above triangles satisfy SAS criteria,

Hence △ UVW ∼ △ XYZ

This criterion is applicable if one side & one angle of each triangle are known.

Basic Proportionality Thoerem (BPT)

Statement: If a line parallel to a side of a triangle intersects the remaining sides in two distinct points, then the line divides the other sides in the same proportion.

Proof:

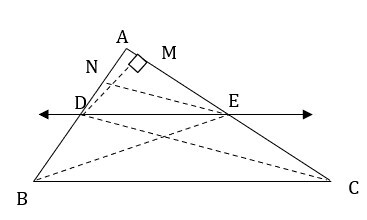
Given: In △ ABC, line DE || line BC

Line DE intersects lines AB & AC at points D & E respectively.

To prove − $\mathrm{\frac{AD}{DB}=\frac{AE}{EC}}$

Construction: Join BE & CD & then draw DM ⊥ AC & EN ⊥AB

Proof: Area of △ADE = $\mathrm{\frac{1}{2}×AD×EN}$

Also, Area of △ BDE = $\mathrm{\frac{1}{2}×DB×EN}$

Area of △ADE = $\mathrm{\frac{1}{2}×AE×DM}$ & Area of △BDE = $\mathrm{\frac{1}{2}×EC×DM}$

△ADE & △BDE have equal height EN

Therefore, $\mathrm{\frac{Area\: of\: \triangle ADE}{Area\: of\: \triangle BDE }=\frac{AD}{DB} …………..(i)}$

Also, △ADE & △DEC have equal height DM

Therefore, $\mathrm{\frac{Area\: of\: \triangle ADE}{Area\: of\: \triangle DEC }=\frac{AE}{EC} …………..(ii)}$

△BDE & △DEC have the same base DE & line BC || line DE.

Therefore, Area of △BDE = Area of △DEC

Therefore, from (i), (ii) & (iii),

$$\mathrm{\frac{AD}{DB}=\frac{AE}{EC}}$$

Solved examples

1) Check whether the following triangles are similar or not? If yes, explain by which test?

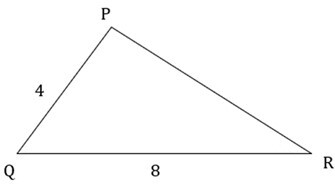
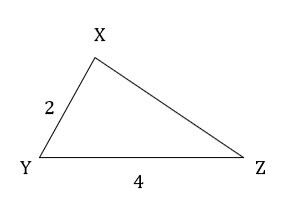
Ans: In △ PQR & △ XYZ

$$\mathrm{\frac{PQ}{XY}=\frac{4}{2}=2 \: \& \: \frac{QR}{YZ}=\frac{8}{4}=2}$$

Therefore,$\mathrm{\frac{PQ}{XY}=\frac{QR}{YZ}}$

Also $\mathrm{\angle M \cong \angle Y}$ …………(Given)

△ PQR ∼ △ XYZ …………( SAS criteria of similarity)

2) In given figure, AB || EF, then prove that △AOB ∼ △ EOF.

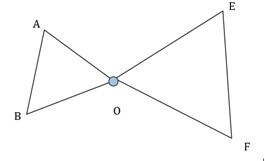
Ans: AB || EF ……..(Given)

$\mathrm{\angle A =\angle F}$ ……..(Alternate angles)

$$\mathrm{\angle B =\angle F}$$

$\mathrm{\angle AOB =\angle EOF}$ ……...( Vertically opposite angles)

Hence △ AOB ∼ △ EOF.

3) 1) In △PQR, line AB || QR

If QA = 4.8 cm, PA = 1.6 cm, BR = 6.4 cm then find PB.

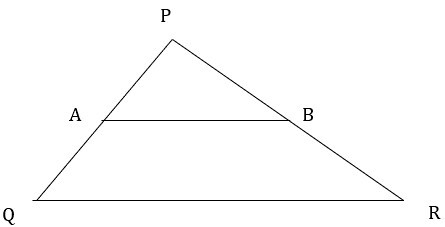
Ans: In △PQR, AB || QR ……..(Given)

By basic proportionality theorem,

$$\mathrm{\frac{PA}{AQ}=\frac{PB}{BR}}$$

$$\mathrm{\frac{1.6}{4.8}=\frac{PB}{6.4}}$$

$$\mathrm{PB=\frac{1.6\times 6.4}{4.8}}$$

$$\mathrm{PB = 2.1 cm}$$

Conclusion

Similarity of a triangle is one of the important proprety of triangle.

If two triangles are said to be similar if their angles are congruent & corresponding sides are in proportion. Basic proportionality theorem was introduced by Greek mathematician Thale. It stated as, if a line drawn parallel to one side of a triangle, it intersects another two sides in distinct two points & divides the side in same proportion.

FAQs

1. What are congruent triangles?

If two corresponding angles & sides of any two triangles are equal then those triangles are said to be congruent triangles.

2. State the types of a triangle which is always similar.

Equilateral triangles & two isosceles right triangles are always similar.

3. State the theorem of areas of similar triangles.

It stated as when two triangles are similar then the ratio of areas of those triangles is equal to the ratio of the squares of their corresponding side.

4. Is the basic proportionality theorem applicable to a scalene triangle?

Yes. The basic proportionality theorem is applicable to all triangles.

5. What are the applications of the basic proportionality theorem?

The basic proportionality theorem is used to prove the following properties −

• Property of an angle bisector of a triangle.

• Property of three parallel lines with their transversals.