Area under the Curve – Calculus

Introduction

The area under a curve between two points is found out by doing a definite integral between the two points. Among the various ways to calculate the area under the curve, the most popular method is the antiderivative method. By determining the equation for the curve, the boundaries of the curve, and the axis enclosing the curve the area under the curve can be calculated. There are formulas to find the area enclosed by a circle, square, rectangle, and other polygons, but the area under the curve can be used to find area for the shapes that do not have predefined formulas. Integration is the tool of integral calculus which helps in solving the area enclosed by a curve. Antiderivatives are helpful in finding the area of an irregular plane. In this tutorial, we will learn about the area enclosed by a curve, about integrals, and some examples which will help in better understanding of the topic.

Integrals

Integrals can be used to calculate the area bounded by a curve, say f(x), between x=a, and x=b. These integrals have limits that define their boundaries under which the sum is calculated for the given function.

Let us assume a function f(x) between [p,q]. The interval between p and q is divided into m sub-intervals having width dx. The formula for finding the value of the definite integral is,

$$\mathrm{Area= \int_p^qf(x)dx=F(q)-F(p).}$$

where F is the antiderivative of f.

Area under a Curve

Among various uses of definite integrals, calculating the area bounded by a curve is one of the most important functions. The area of the curve is calculated using different formulae for two axes (X- and Y-axis), which act as boundaries for the given curve.

Area of a curve with a boundary as X-axis −

In the graph below, the area is bound by a curve, say f(x), between point x=a, and point x=b. We can use definite integrals to calculate the area of the rectangular under the curve shown in the graph. The area can be given by −

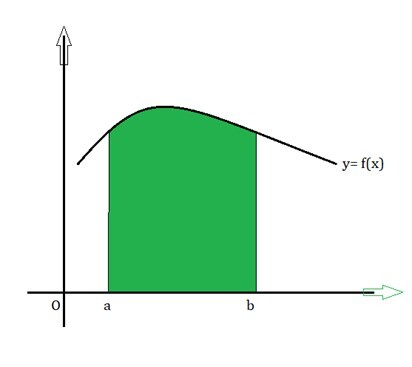
$$\mathrm{Area= \int_a^bf(x)dx}$$

Similarly, the area is bound by a curve say f(y) between point y=a, and point y=b. We can use definite integrals to calculate the area of the rectangular under the curve shown in the graph. The area can be given by −

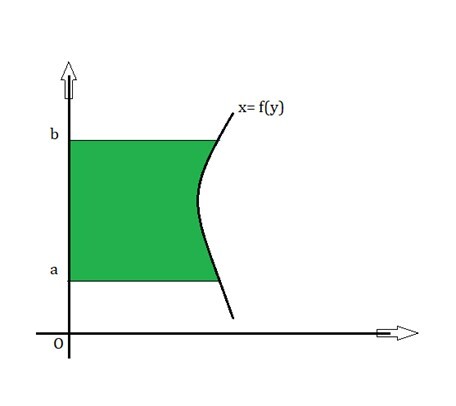
$$\mathrm{Area= \int_a^bf(y)dy}$$

Area between Two Curves

Similarly for the Y-axis, let dy be the division of area into segments parallel to the X-axis between the values of y, a and b; and calculate the summation of the area of those segments. These rectangular strips will have the width "dy" and height f(y)-g(y). The area of segment is given by

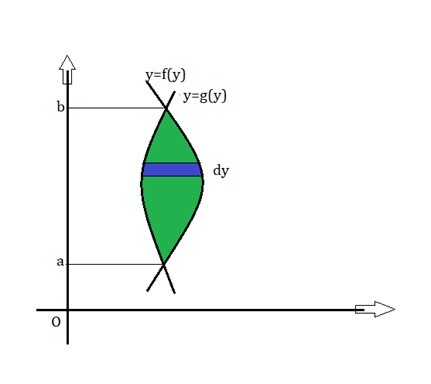
$$\mathrm{Area= \int_a^b[f(y)-g(y)]dy}$$

Similarly for the X-axis, let dx be the division of area into segments parallel to the y-axis between the values of x, a and b; and calculating the summation of the area of those segments. These rectangular strips will have the width "dx" and height f(x)-g(x). The area of segment is given by

$$\mathrm{Area= \int_a^b[f(x)-g(x)]dx}$$

Solved Examples

1)For a curve f(x)=x²+3, determine the area bounded by the curve, the x-axis and lines x=1 and x=4.

Answer: The area under the curve with X-axis as the boundary is given by

$$\mathrm{Area= \int_p^qf(x)dx=F(p)-F(q).}$$

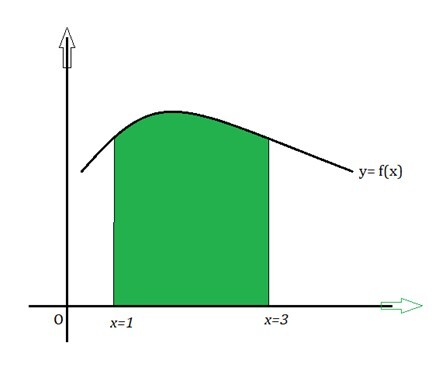
putting f(x)= p=1 and q=3 in the above equation,

$$\mathrm{ Area = \int_1^3f(x)dx=\int_1^3(x^2+3) }$$

$$\mathrm{ =[\frac{x^3}{3}+3x]_1^3}$$

$$\mathrm{=[(9/3)+9-((1/3)+3)]}$$

$$\mathrm{=12-\frac{10}{3}}$$

Area of the curve =26/3 square units.

2)Find the area between two curved line with equations f(y)=y² and g(y)=y³, between points y=0 and y=1.

Answer:

Area between two curves can be given by

$$\mathrm{Area= \int_a^b[f(y)-g(y)]dy.}$$

Putting the values a=0,b=1 and f(y)=y^2, g(y)=y^3 in the above equation,

$$\mathrm{Area= ∫_0^1[(y^2)-(y^3)]dy}$$

$$\mathrm{=[\frac{y^3}{3}-\frac{y^4}{4}]_0^1}$$

$$\mathrm{=[1/3-1/4]}$$

Area =1/12 square units.

3)Find the area under the curve x=(y-2)² and line x+2y=7 which intersect at two points P(-1,9) and Q(3,1).

Answer:

For the equation of the curve x=(y-2)²

$$\mathrm{x=y^2+4-4y}$$

$$\mathrm{f(y)=y^2+4-4y.}$$

For the equation of the line x+2y=7

$$\mathrm{x=7-2y}$$

$$\mathrm{g(y)=7-2y.}$$

The area under the curve and a line is given by,

$$\mathrm{Area= \int_a^b[f(y)-g(y)]dy.}$$

Putting the value of x coordinates (-1,3) as a and b,

$$\mathrm{Area= \int_{-1}^3[(7-2y)-(y^2+4-4y)]dy}$$

$$\mathrm{=∫_{-1}^3[(-y^2+2y+3)]dy}$$

$$\mathrm{=-[\frac{y^3}{3}-2 \frac{y^2}{2}-3y]_{-1}^3}$$

$$\mathrm{=-\frac{1}{3} [y^3-3y^2-9y]_{-1}^3}$$

$$\mathrm{=-\frac{1}{3} [(3^3-3(3^2)-9(3))-((-1)^3-3(-1)^2-9(-1))]}$$

$$\mathrm{=-\frac{1}{3}(-32)}$$

Area between the curve and the line=32/3 square units.

4)For area enclosed by $\mathrm{\frac{x^2}{16}+\frac{y^2}{9}=1}$, find the area under the curve.

Answer: For the given equation, we can write the equation in terms of a. we can also write the given equation as

$$\mathrm{\frac{x^2}{16}+\frac{y^2}{9}=1}$$

$$\mathrm{9x^2+16y^2=144}$$

$$\mathrm{y^2=\frac{(144-9x^2)}{9}}$$

$$\mathrm{y^2=\sqrt{\frac{(144-9x^2)}{9}}}$$

$$\mathrm{y=\frac{3}{4} \sqrt{(16-x^2)}}$$

An ellipse is divided into 4 quadrants. By calculating the area under the curve for 1 quadrant and multiplying by 4, we can get the total area enclosed by the curve.

$$\mathrm{Area=4×\int_0^4\frac{3}{4} \sqrt{(16-x^2)}}$$

Substituting x=4sinθ. We can also write it as dx=4cosθ dθ

upper and lower limit changes to 0 and Π/2.

We know that area

$$\mathrm{A=4×\int_0^{Π/2}\frac{3}{4} \sqrt{(16-(4sinθ)^2)}.4cosθ.dθ}$$

$$\mathrm{A=12×\int_0^{Π/2}\sqrt{(16-16(sinθ)^2)}.cosθ.dθ}$$

$$\mathrm{A=48×\int_0^{Π/2}\sqrt{(1-(sinθ)^2)}.cosθ.dθ}$$

$$\mathrm{A=48×\int_0^{Π/2}cosθ.cosθ.dθ}$$

$$\mathrm{A=48×\int_0^{Π/2}\frac{1+cos2θ}{2}dθ}$$

$$\mathrm{A=48×\frac{Π}{4}}$$

$$\mathrm{A=12π}$$

5)Calculate the area of a circle using the area under the curve.

Answer: A circle is divided into 4 quadrants. By calculating the area under the curve for 1 quadrant and multiplying by 4, we can get the total area enclosed by the circle.

Equation of a circle can be given by

$$\mathrm{p^2+q^2=r^2}$$

Writing the equation as a curve equation, we can write:

$$\mathrm{q=\sqrt{r^2-p^2}}$$

Integrating the above equation with lower and upper limits as 0 and r, respectively.

$$\mathrm{A=4.\int_0^rq.dp}$$

$$\mathrm{A=4.\int_0^r \sqrt{r^2-p^2}.dp}$$

Integrating the above equation and applying the limit from 0 to r, we get

$$\mathrm{A=4.(\frac{r^2}{2})\frac{π}{2}}$$

$$\mathrm{A=πr^2}$$

Therefore, the area under the curve for a circle is πr²

Conclusion

In this tutorial, we learned about Integrations and how Integration can be used to find the Area under a curve or Area between two curves. Integral calculus has been used for solving complex problems. Area under the curve utilises definite integrals in order to calculate other parameters for the bounded space. For example, drawing a velocity-time equation on a graph. By determining the boundaries of the equation, we can estimate the distance travelled. The area under a curve is calculated with the help of definite integrals. Area under a curve can be given by

$$\mathrm{Area = ∫_p^qf(x)dx=F(q)-F(p).}$$

FAQs

1. Is the value of the area between curves always non-negative?

Yes, the area between two curves can always be positive or zero because it is an absolute value.

2. How can we calculate the area between two curves?

Area between two curves f(x) and g(x) with two intersection point “a” and “b” can be calculated by −

$$\mathrm{Area= \int_a^b[f(x)-g(x)]dx}$$

3. What does area under the curve in a velocity-time graph represent?

The area under the curve in a velocity-time graph represents the total distance covered.

4. What are definite integrals?

Definite integrals are used as a tool to calculate the area between curves with given equations.

5. What are the uses of calculating the area under the curve?

The area under the curve is used to calculate areas of shapes with boundaries. It can be used to find the area of the irregular shapes in a two-dimensional space.