Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Area of squares formed by joining midpoints repeatedly in C?
Area of a square is equal to the product of sides of the square.
We are considering a figure in which the midpoints of sides of each square make another square. And so on until a specific number of squares.
This figure shows a square made by joining the midpoints of a square.
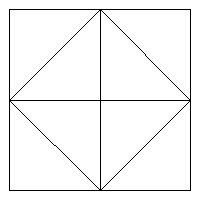
For this figure the let the side be a,
The length of side of inner square will be
L2 = (a/2)2 + (a/2)2
L2 = a2(1/4 + 1/4) = a2(1/2) = a2/2
L = a2/ (\sqrt{2}).Area of square2 = L2 = a2/2.
For the next square, the area of square 3 = a2/4
Lets take an example, tge
Now are we can infer from here about areas of consecutive squares,
a2, a2/2, a2/4, a2/8, …..
This is a GP with a2 being the first term of the and ½ being the common ratio.
Example
#include <stdio.h>
#include <math.h>
int main() {
double L = 2, n = 10;
double firstTerm = L * L;
double ratio = 1 / 2.0;
double are = firstTerm * (pow(ratio, 10)) ;
printf("The area of %lfth square is %lf", n , sum);
return 0;
}Output
The area of 10th square is 0.003906
Updated on: 03-Oct-2019
56 Views
Advertisements