Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Minimum Cost Polygon Triangulation
When nonintersecting diagonals are forming a triangle in a polygon, it is called the triangulation. Our task is to find a minimum cost of triangulation.
The cost of triangulation is the sum of the weights of its component triangles. We can find the weight of each triangle by adding their sides, in other words, the weight is the perimeter of the triangle.
Input and Output
Input:
The points of a polygon. {(0, 0), (1, 0), (2, 1), (1, 2), (0, 2)}
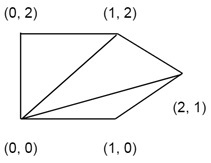Output:
The total cost of the triangulation. Here the cost of the triangulation is 15.3006.Algorithm
minCost(polygon, n)
Here cost() will be used to calculate the perimeter of a triangle.
Input: A set of points to make a polygon, and a number of points.
Output − Minimum cost for triangulation of a polygon.
Begin if n < 3, then return 0 define table or order n x n i := 0 for gap := 0 to n-1, do for j := gap to n-1, do if j < i+2, then table[i,j] := 0 else table[i, j] = ∞ for k := i+1 to j-1, do val := table[i, k] + table[k, j] + cost(i, j, k) if table[i, j] > val table[i, j] := val i := i + 1 done done return table[0, n-1] End
Example
#include <iostream>
#include <cmath>
#include <iomanip>
#define MAX 1000000.0
using namespace std;
struct Point {
int x, y;
};
double min(double x, double y) {
return (x <= y)? x : y;
}
double dist(Point p1, Point p2) { //find distance from p1 to p2
return sqrt(pow((p1.x-p2.x),2) + pow((p1.y-p2.y),2));
}
double cost(Point triangle[], int i, int j, int k) {
Point p1 = triangle[i], p2 = triangle[j], p3 = triangle[k];
return dist(p1, p2) + dist(p2, p3) + dist(p3, p1); //the perimeter of the triangle
}
double minimumCost(Point polygon[], int n) {
if (n < 3) //when polygon has less than 3 points
return 0;
double table[n][n];
for (int gap = 0; gap < n; gap++) {
for (int i = 0, j = gap; j < n; i++, j++) {
if (j < i+2)
table[i][j] = 0.0;
else {
table[i][j] = MAX;
for (int k = i+1; k < j; k++) {
double val = table[i][k] + table[k][j] + cost(polygon,i,j,k);
if (table[i][j] > val)
table[i][j] = val; //update table data to minimum value
}
}
}
}
return table[0][n-1];
}
int main() {
Point points[] = {{0, 0}, {1, 0}, {2, 1}, {1, 2}, {0, 2}};
int n = 5;
cout <<"The minimumcost: " <<minimumCost(points, n);
}Output
The minimumcost: 15.3006
Updated on: 17-Jun-2020
494 Views
Advertisements