Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Maximum sum rectangle in a 2D matrix
A matrix is given. We need to find a rectangle (sometimes square) matrix, whose sum is maximum.
The idea behind this algorithm is to fix the left and right columns and try to find the sum of the element from the left column to right column for each row, and store it temporarily. We will try to find top and bottom row numbers. After getting the temporary array, we can apply the Kadane’s Algorithm to get maximum sum sub-array. With it, the total rectangle will be formed.
Input and Output
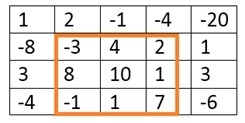
Input: The matrix of integers. 1 2 -1 -4 -20 -8 -3 4 2 1 3 8 10 1 3 -4 -1 1 7 -6 Output: The top left point and bottom right point of the submatrix, and the total sum of the submatrix. (Top, Left) (1, 1) (Bottom, Right) (3, 3) The max sum is: 29
Algorithm
kadaneAlgorithm(array, start, end, n)
Input: The array will hold sums, start and end points, number of elements.
Output − Find the starting and ending point.
Begin sum := 0 and maxSum := - ∞ end := -1 tempStart := 0 for each element i in the array, do sum := sum + array[i] if sum < 0, then sum := 0 tempStart := i + 1 else if sum > maxSum, then maxSum := sum start := tempStart end := i done if end ≠ -1, then return maxSum maxSum := array[0], start := 0 and end := 0 for each element i from 1 to n of array, do if array[i] > maxSum, then maxSum := array[i] start := i and end := i done return maxSum End
maxSumRect(Matrix)
Input: The given matrix.
Output: the Maximum sum of the rectangle.
Begin maxSum := - ∞ define temp array, whose size is same as row of matrix for left := 0 to number of columns in the Matrix, do till temp array with 0s for right := left to column of matrix -1, do for each row i, do temp[i] := matrix[i, right] done sum := kadaneAlgorithm(temp, start, end, number of rows) if sum > maxSum, then maxSum := sum endLeft := left endRight := right endTop := start endBottom := end done done display top left and bottom right corner and the maxSum End
Example
#include<iostream>
#define ROW 4
#define COL 5
using namespace std;
int M[ROW][COL] = {
{1, 2, -1, -4, -20},
{-8, -3, 4, 2, 1},
{3, 8, 10, 1, 3},
{-4, -1, 1, 7, -6}
};
int kadaneAlgo(int arr[], int &start, int &end, int n) { //find max sum and starting and ending location
int sum = 0, maxSum = INT_MIN;
end = -1; //at first no place is selected
int tempStart = 0; //starting from 0
for (int i = 0; i < n; i++) {
sum += arr[i];
if (sum < 0) {
sum = 0;
tempStart = i+1;
}else if (sum > maxSum) { //get maximum sum, and update start and end index
maxSum = sum;
start = tempStart;
end = i;
}
}
if (end != -1)
return maxSum;
//when all elements are negative in the array
maxSum = arr[0];
start = end = 0;
// Find the maximum element in array
for (int i = 1; i < n; i++) {
if (arr[i] > maxSum) {
maxSum = arr[i];
start = end = i;
}
}
return maxSum;
}
void maxSumRect() {
int maxSum = INT_MIN, endLeft, endRight, endTop, endBottom;
int left, right;
int temp[ROW], sum, start, end;
for (left = 0; left < COL; left++) {
for(int i = 0; i<ROW; i++)//temp initially holds all 0
temp[i] = 0;
for (right = left; right < COL; ++right) {
for (int i = 0; i < ROW; ++i) //for each row, find the sum
temp[i] += M[i][right];
sum = kadaneAlgo(temp, start, end, ROW); //find sum of rectangle (top, left) and (bottom right)
if (sum > maxSum) { //find maximum value of sum, then update corner points
maxSum = sum;
endLeft = left;
endRight = right;
endTop = start;
endBottom = end;
}
}
}
cout << "(Top, Left) ("<<endTop<<", "<<endLeft<<")"<<endl;
cout << "(Bottom, Right) ("<<endBottom<<", "<<endRight<<")"<<endl;
cout << "The max sum is: "<< maxSum;
}
int main() {
maxSumRect();
}Output
(Top, Left) (1, 1) (Bottom, Right) (3, 3) The max sum is: 29
Updated on: 17-Jun-2020
1K+ Views
Advertisements