
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is Effective Isotropic Radiated Power (EIRP)?
A wireless link budget, in general, estimates the possible losses that will be encountered by the signal being transmitted and adjustments are made on the design parameters to combat the effects of such losses. EIRP is commonly used in wireless link budget calculations to specify the power level required for transmission.
How would you define Effective Isotropic Radiated Power (EIRP)?
As the name suggests, the EIRP takes power transmitted by an isotropic source as the reference. EIRP combines the power of the transmitting antenna and its gain. EIRP is expressed as the product of the power of the transmitting antenna and its gain.
$$EIRP=P_{t}G_{t}$$
Pt is the power of the transmitting antenna and Gt is the gain of the transmitting antenna.
In essence, the product of the power radiated and the gain of a realizable antenna is compared with the product of the power radiated and the gain of an isotropic source. Since an isotropic source radiates equally in all directions, its gain is unity (or 0 dB).
EIRP OF ISOTROPIC AND REALIZABLE ANTENNA
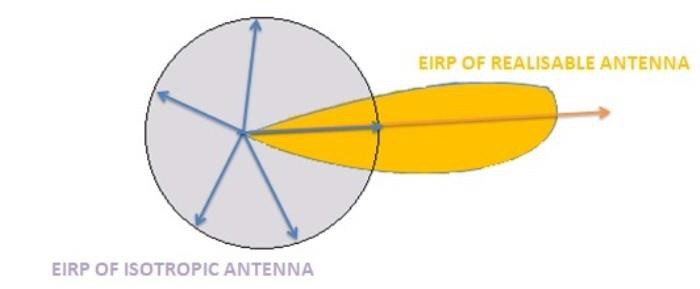
The figure shows the EIRP of an isotropic radiator and a realizable antenna. We can observe that the EIRP of a realizable antenna would usually be greater than the EIRP of an isotropic radiator.
EIRP of realizable antenna > EIRP of isotropic
Formula of EIRP
The EIRP of an isotropic radiator and a realizable antenna is expressed as below −
$$EIRP_{ISOTROPIC}=P_{ISOTROPIC}\times\:G_{ISOTROPIC}$$
$$EIRP_{SYSTEM}=P_{ANTENNA}\times\:G_{ANTENNA}$$
EIRP is expressed as an absolute value as well as logarithmic value in base 10 scale.
$$EIRP_{dBW}=10\:log_{10}(P_{t}G_{t})$$
$$EIRP_{dBW}=10\:log_{10}(P_{t})+10\:log_{10}(G_{t})=P_{t(dB)}+G_{t(dB)}$$
Since the gain of the antenna is essentially a unitless quantity in both the absolute and logarithmic scale, EIRP will take the unit of power and when expressed in the logarithmic scale, we use dBW which means decibel power with reference to 1 W. Here, 1 W is the reference power. The representation dBmW is also used where 1 mW is taken as the reference power.
dBW & dBmW
These are representing powers in the logarithmic base 10 scale. We take the ratios of two quantities having the unit of power and map it on to the logarithmic scale. In this ratio, one of the power quantities is taken as the reference power.
$$P_{dBW}=10\:log_{10}(\frac{P_{W}}{1W})$$
$$P_{dBmW}=10\:log_{10}(\frac{P_{W}}{1mW})$$
Negative dBm AND dBW
If PdBW and PdBmW take negative values, it implies that, the measured power is less than the reference power.
If the specified power level is -20 dBm, this means that the measured or received power level is one-hundredth of the reference power.
$$-20dBm=10log_{10}(\frac{P}{1mW})$$
$$log_{10}(\frac{P}{1mW})=-2$$
$$(\frac{P}{1mW})=10^{-2};\:P=\frac{1}{100}(1mW)=0.01mW$$
EIRP EXAMPLE
In a satellite communication, the transmitting antenna radiates a power of 20 W. The gain of the antenna is 15 dBi. Calculate the EIRP.
Soln. We convert the antenna gain back to the absolute scale.
$$15=10log_{10}(X)$$
$$X=10^{1.5}=31.622$$
$$EIRP=P_{t}.G_{t}=(20W)(31.622)=632.44W=28.01dBW$$

