Theano - Expression for Matrix Multiplication

---

---

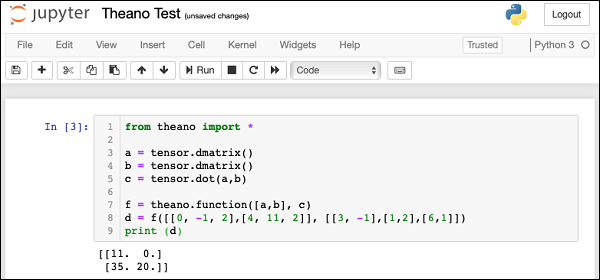
We will compute a dot product of two matrices. The first matrix is of dimension 2 x 3 and the second one is of dimension 3 x 2. The matrices that we used as input and their product are expressed here −

$$\begin{bmatrix}0 & -1 & 2\\4 & 11 & 2\end{bmatrix} \:\begin{bmatrix}3& -1 \\1 & 2 \\35 & 20 \end{bmatrix}=\begin{bmatrix}11 & 0 \\35 & 20 \end{bmatrix}$$

Declaring Variables

To write a Theano expression for the above, we first declare two variables to represent our matrices as follows −

a = tensor.dmatrix()
b = tensor.dmatrix()

The dmatrix is the Type of matrices for doubles. Note that we do not specify the matrix size anywhere. Thus, these variables can represent matrices of any dimension.

Defining Expression

To compute the dot product, we used the built-in function called dot as follows −

c = tensor.dot(a,b)

The output of multiplication is assigned to a matrix variable called c.

Defining Theano Function

Next, we define a function as in the earlier example to evaluate the expression.

f = theano.function([a,b], c)

Note that the input to the function are two variables a and b which are of matrix type. The function output is assigned to variable c which would automatically be of matrix type.

Invoking Theano Function

We now invoke the function using the following statement −

d = f([[0, -1, 2], [4, 11, 2]], [[3, -1],[1,2], [6,1]])

The two variables in the above statement are NumPy arrays. You may explicitly define NumPy arrays as shown here −

f(numpy.array([[0, -1, 2], [4, 11, 2]]),
numpy.array([[3, -1],[1,2], [6,1]]))

After d is computed we print its value −

print (d)

You will see the following output on the output −

[[11. 0.]
[25. 20.]]

Full Program Listing

The complete program listing is given here:
from theano import *
a = tensor.dmatrix()
b = tensor.dmatrix()
c = tensor.dot(a,b)
f = theano.function([a,b], c)
d = f([[0, -1, 2],[4, 11, 2]], [[3, -1],[1,2],[6,1]])
print (d)

The screenshot of the program execution is shown here −