- DCN Tutorial
- Data Comm & Networks Home
- DCN - Overview
- DCN - Computer Network Types
- DCN - Network LAN Technologies
- DCN - Computer Network Topologies
- DCN - Computer Network Models
- DCN - Computer Network Security
- Physical Layer
- DCN - Physical Layer Introduction
- DCN - Digital Transmission
- DCN - Analog Transmission
- DCN - Transmission media
- DCN - Wireless Transmission
- DCN - Multiplexing
- DCN - Network Switching
- Data Link Layer
- DCN - Data Link Layer Introduction
- DCN - Error detection and Correction
- DCN - Data Link Control & Protocols
- Network Layer
- DCN - Network Layer Introduction
- DCN - Network Addressing
- DCN - Routing
- DCN - Internetworking
- DCN - Network Layer Protocols
- Transport Layer
- DCN - Transport Layer Introduction
- DCN - Transmission Control Protocol
- DCN - User Datagram Protocol
- Application Layer
- DCN - Application Layer Introduction
- DCN - Client-Server Model
- DCN - Application Protocols
- DCN - Network Services
- DCN Useful Resources
- DCN - Quick Guide
- DCN - Useful Resources
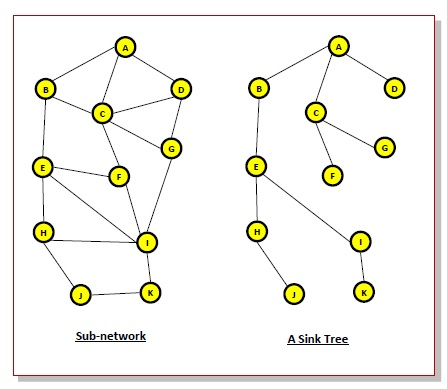
Sink Tree in Computer Networks
Definition
Sink trees of a given node in a computer network is a tree formed by connecting the node with all the other nodes of in the network with the optimal path, or more precisely the shortest path. Or, in other words, a sink tree is a minimal cost tree formed with the given node as the destination and all other nodes as sources. A popular measure for the path or the cost is the number of hops.
Explanation
The sink tree follows from the optimality principle. According to it, in a network of routers for data transmission, if a router ‘J’ lies on the optimal path from router ‘I’ to router ‘K’, then the optimal path from router ‘J’ to router ‘K’ also falls along the same route.
As a direct consequence the optimality principle, it can be seen that the set of optimal routes from all source nodes to the destination node form a tree with the destination as the root node.
A sink tree may not be unique. There can exist more than one sink trees having same path length. The objective of routing algorithms is to find the sink trees for all nodes in the network. Since, links and nodes may go down and revive during data transmission, the alternative sink trees and the paths are also made available to the nodes.
Being a tree, a sink tree does not contain any loops or cycles. So each packet can be delivered within a finite number of hops. Also, a packet will not be infinitely rotated within a subnet.
Example
The diagram below shows a network on the left side and the sink tree on the right with node A as the root node.
- Related Articles
- Hamming Code in Computer Networks
- Circuit Switching in Computer Networks
- Performance Problems in Computer Networks
- Uses of Computer Networks
- Computer Networks Cheat Sheet
- Error correcting codes in Computer Networks
- Multiple Access Protocols in Computer Networks
- The Optimality Principle in Computer Networks
- Forward Error Correction in Computer Networks
- What is IPsec in computer networks?
- Types of Firewalls in Computer Networks
- What is Tunnelling in Computer Networks?
- What is NAT in computer networks?
- What is Blocking Networks and Non-Blocking Networks in Computer Architecture?
- What is bit stuffing in computer networks?
