Section Formula in 3D

Introduction

The section formula can be applied to a line segment located in 2D or 3D. The division of a line segment is a method or process in which the line segment is divided into several parts (equal or non-equal). Points are used to divide a line segment. It is an important method used in coordinate geometry to determine the centroid, incenter, and excenter of a triangle. In this tutorial, we will discuss the 3D geometry, section formula, and distance formula with solved examples.

3D Coordinate Geometry

The 3D coordinate geometry represents the geometrical figures in 3D space. It requires three coordinates to represent the position of any point in 3D plane. In addition, the three coordinates tell us about the position of the point on the X- axis, Y-axis, and Z-axis. The intersection of the three axis is called origin (as shown in the figure). In real life, we see various objects, which have height, depth, and breadth. These are known as 3D geometries.

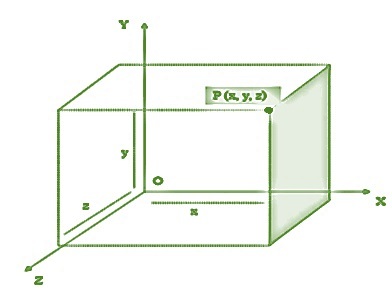
Section Formula in 3D Geometry

The section formulae are classified based on the relative location of the point with respect to the line segment. There are two types of sections formula that exist in coordinate geometry such as −

• Internal section formula

• External section formula

Now, we will discuss the formula of each section in detail.

Internal section formula:

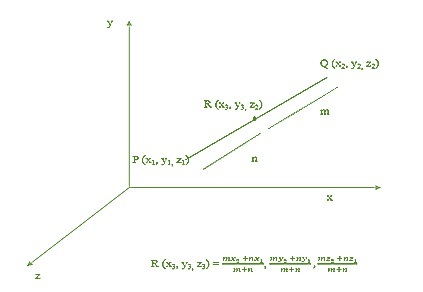
In this type of division, the line segment is internally divided into two parts by a point. For example, consider a line segment having coordinates of the end point

$\mathrm{P(x_{1}y_{1}z_{1})\:and\:Q(x_{2}y_{2}z_{2}).\:A\:point\:R(x_{3}y_{3}z_{3})}$is internally divided by the line segment in a ratio of m:n (as shown in the figure). Now, the coordinate of the point $\mathrm{R(x_{3}y_{3}z_{3})}$ can be determined using the following formula.

$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{mx_{2}\:+\:nx_{1}}{m\:+\:n}\:,\:\frac{my_{2}\:+\:ny_{1}}{m\:+\:n}\:,\:\frac{mz_{2}\:+\:nz_{1}}{m\:+\:n})}$

If we separate the coordinates, we will get

𝑥-axis coordinate $\mathrm{=\:\frac{mx_{2}\:+\:nx_{1}}{m\:+\:n}}$ , 𝑦-axis coordinate $\mathrm{=\:\frac{my_{2}\:+\:ny_{1}}{m\:+\:n}}$ z-axis coordinates $\mathrm{\frac{mz_{2}\:+\:nx_{1}}{m\:+\:n}}$

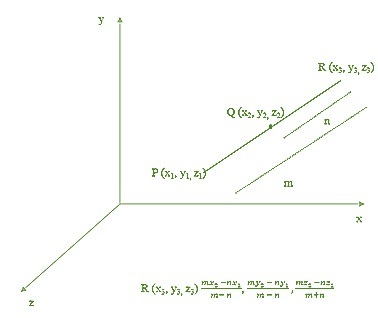
External section formula

In this type of division, the line segment is externally divided into two parts by a point. For example, consider a line segment having coordinates of the end point $\mathrm{P(x_{1},y_{1}z_{1})\:and\:Q(x_{2},y_{2},z_{2})\:.\:A\:point\:R(x_{3},y_{3},z_{3})}$ is externally divided by the line segment in a ratio of m:n (as shown in the figure). Now, the coordinate of the point $\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})}$ can be determined using the following formula.

$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{mx_{2}\:-\:nx_{1}}{m\:-\:n}\:,\:\frac{my_{2}\:-\:ny_{1}}{m\:-\:n}\:,\:\frac{mz_{2}\:-\:nz_{1}}{m\:-\:n})}$

If we separate the coordinates, we will get

𝑥-axis coordinate $\mathrm{=\:\frac{mx_{2}\:-\:nx_{1}}{m\:-\:n}}$ , 𝑦-axis coordinate $\mathrm{=\:\frac{my_{2}\:-\:ny_{1}}{m\:-\:n}}$ z-axis coordinates $\mathrm{\frac{mz_{2}\:-\:nx_{1}}{m\:-\:n}}$

Distance Formula in 3D Geometry (Brief)

Let’s consider the coordinates of the end points of a line segment are $\mathrm{P(x_{1},y_{1},z_{1})\:and\:Q(x_{2},y_{2},z_{2})}$ Through points P and Q, we draw planes parallel to the rectangular coordinates such that $\mathrm{\angle\:QPR\:=\:90°\:and\:\angle\:PSR\:=\:90°}$

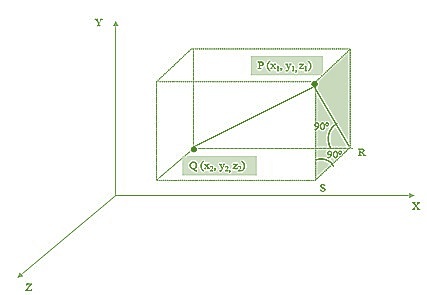
Using Pythagoras theorem in triangle PQR,

$\mathrm{PQ^{2}\:=\:PR^{2}\:+\:QR^{2}..................(1)}$

Similarly, Using Pythagoras theorem in triangle PSR,

$\mathrm{PR^{2}\:=\:PS^{2}\:+\:RS^{2}..................(2)}$

Putting the value of $\mathrm{PR^{2}}$ in Eq. (1), we get

$\mathrm{PQ^{2}\:=\:PS^{2}\:+\:RS^{2}\:+\:QR^{2}.................(3)}$

Using the coordinates of the points, $\mathrm{PS\:=\:y_{2}\:-\:y_{1}\:,\:RS\:=\:z_{2}\:-\:z_{1}\:,\:QR\:=\:x_{2}\:-\:x_{1}}$

Now, putting the value of PS, RS and QR in Eq. (3)

$$\mathrm{\Longrightarrow\:PQ^{2}\:=\:(y_{2}\:-\:y_{1})^{2}\:+\:(z_{2}\:-\:z_{1})^{2}\:+\:(x_{2}\:-\:x_{1})^{2}}$$

$$\mathrm{\Longrightarrow\:PQ\:=\:\sqrt{(x_{2}\:-\:x_{1})^{2}\:+\:(y_{2}\:-\:y_{1})^{2}\:+\:(z_{2}\:-\:z_{1})^{2}}}$$

Solved Examples

Example 1

Consider the coordinates of the endpoints of a line segment are (-1, -3, 2), (0, 11, 5). Find the coordinate of the point which divides the above line segment internally in a ratio of 2:1.

Solution −

According to the question,

The coordinates of the endpoints of the line segment $\mathrm{=\:(-1\:,\:-3\:,\:2)\:,\:(0\:,11\:,\:5)}$

Comparing with the standard coordinates, $\mathrm{x_{1}\:=\:-1\:,\:y_{1}\:=\:-3\:,\:z_{1}\:=\:2\:,\:x_{2}\:=\:0\:,\:y_{2}\:.\:z_{2}\:=\:5}$

The internal division ratio = 2:1 (Here, m= 2, n=1)

Suppose $\mathrm{R(x_{3},y_{3},z_{3})}$ be the required point.

Using the internal section formula,

$$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{mx_{2}\:+\:nx_{1}}{m\:+\:n}\:,\:\frac{my_{2}\:+\:ny_{1}}{m\:+\:n}\:,\:\frac{mz_{2}\:+\:nz_{1}}{m\:+\:n})}$$

$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{2\:\times\:(0)\:+\:1\:\times\:(-1)}{2\:+\:1}\:,\:\frac{2\:\times\:(0)\:+\:1\:\times\:(-1)}{2\:+\:1}\:,\:\frac{2\:\times\:5\:+\:1\:\times\:2}{2\:+\:1})}$

$$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{-1}{3},\frac{19}{3},4)}$$

∴The coordinated of the required point is $\mathrm{(\frac{-1}{3},\frac{19}{3},4)}$

Example 2

The coordinates of the endpoints of a line segment are (1, -4, -9) and (8, -3, -1).Find the coordinate of the point which divides the above line segment externally in a ratio of 3:5.

Solution −

It is given that,

The coordinates of the endpoints of the line segment = (1, -4, -9) and (8, -3, -1)

Comparing with the standard coordinates, $\mathrm{x_{1}\:=\:1,y_{1}\:=\:-4,z_{1}\:=\:-9,x_{2}\:=\:8,y_{2}\:=\:-3,z_{2}\:=\:-1}$

The external division ratio $\mathrm{=\:3\colon\:5\:(m\:=\:3\:,\:n\:=\:5)}$

Using the external section formula,

$$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{mx_{2}\:-\:nx_{1}}{m\:-\:n}\:,\:\frac{my_{2}\:-\:ny_{1}}{m\:-\:n}\:,\:\frac{mz_{2}\:-\:nz_{1}}{m\:-\:n})}$$

$$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{3\:\times\:-\:5\:\times\:1}{3\:-\:5},\frac{3\:\times\:(-3)\:-\:(-4)}{3\:-\:5},\frac{3\:\times\:(-1)\:-\:5\:\times\:(-9)}{3\:-\:5})}$$

$$\mathrm{R(x_{3}\:,\:y_{3}\:,\:z_{3})\:=\:(\frac{-19}{2},\frac{-11}{2},21)}$$

∴The coordinated of the required point is $\mathrm{(\frac{-19}{2},\frac{-11}{2},21)}$

Example 3

Check whether the given points are collinear or not.$\mathrm{P(-1,0,7)\:,Q(3,2,1)\:,\:R(5,3,-2)}$

Solution −

If the given points are collinear, the summation of the distance of two line segments will be the third distance.

Now, using the 3D distance formula

$\mathrm{PQ\:=\:\sqrt{(3\:-\:(-1))^{2}\:+\:(2\:-\:0)^{2}\:+\:(1\:-\:7)^{2}}}$

$$\mathrm{\Longrightarrow\:PQ=\:\sqrt{16\:+\:4\:36}\:=\:\sqrt{}56}\:=\:2\sqrt{}14$$

$\mathrm{QR\:=\:\sqrt{(5\:-\:3)^{2}\:+\:(3\:-\:2)^{2}\:+\:(-2\:-\:1)^{2}}}$

$$\mathrm{\Longrightarrow\:QR=\:\sqrt{4\:+\:1\:+\:9}\:=\:\sqrt{14}}$$

$\mathrm{PR\:=\:\sqrt{(5\:-\:(-1))^{2}\:+\:(3\:-\:0)^{2}\:+\:(-2\:-\:7)^{2}}}$

$$\mathrm{\Longrightarrow\:QR\:=\:\sqrt{36\:+\:9\:+\:81}\:=\:\sqrt{126}\:=\:3\sqrt{14}}$$

Since $\mathrm{PQ\:+\:QR\:=\:PR}$ ,therefore the given three points are collinear.

Word Problems

Problem 1: The coordinates of the endpoints of a line segment are (8, 0, -1) and (- 2, -7, -5). Find the coordinate of the point which divides the above line segment externally and internally in a ratio of 7:10.

Problem 2: Find the coordinate of the point on the z-axis, which is equidistant from the points (10, 2, 1) and (-5, -7, 2).

Conclusion

The present tutorial gives a brief introduction about the division of line segments in 3D geometry using the section formula. In addition, the formula to determine the distance between two points has been briefly described. Moreover, some solved examples have been provided for better clarity of this concept. In conclusion, the present tutorial may be useful for understanding the section formula in 3D

FAQs

1. What will be the division ratio if a point is the middle of the line segment?

If the point is a mid-point of the line segment, it must divide the ligament into two equal parts. In this case, the ratio, i.e., m: n, will be 1:1.

2. Can the ratio m: n be negative?

Yes. In external division, the ratio m: n is a negative value.

3. Can the section formula be applied to 2D geometries?

Yes. In two-dimensional coordinate geometry, each point has two coordinates in the x and y directions.

4. What is the difference between the section formula and the midpoint formula?

In the section formula, the point divides the line segment in any arbitrary ratio, i.e., m: n. However, in the case of the mid-point formula, the point divides the line segment in a ratio of 1:1.

5. Can the distance between two points be negative?

No. The distance between two points is always a positive integer.