Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Reorder Routes to Make All Paths Lead to the City Zero in C++
Suppose there are n different cities those are numbered from 0 to n-1 and there are also n-1 roads such that there is only one way to travel between two different cities. Suppose the ministry of transport decided to orient the roads in one direction because they are too narrow.
Here the roads are represented by connections where connections[i] = [a, b] this represents a road from city a to b.
If there is a big event in the capital (city numbered as 0), and many people want to travel to this city. We have to perform some reorienting task on some roads such that each city can visit the city 0. We have to find the minimum number of edges changed.
So, if the input is like 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]],
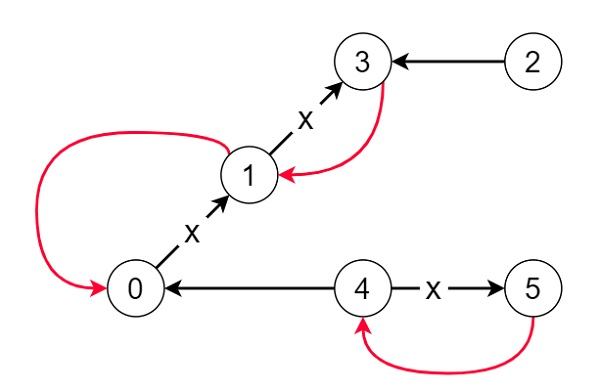
then the output will be 3, as we have to change the direction of edges show in red such that each node can reach the capital.
To solve this, we will follow these steps −
Define two array of lists graph1, graph2 of size N = 5*10^4 + 5
From the main method do the following −
Define one map in
for each element it in e, do
insert it[1] at the end of graph1[it[0]]
insert it[0] at the end of graph2[it[1]]
Define an array dist of size n and fill this with N + 10
ret := 0, in[0] := 0, dist[0] := 0
Define one queue q
insert 0 into q
Define one set visited
insert 0 into visited
while (not q is empty), do −
node := first element of q
delete element from q
ret := ret + dist[node]
for each element it in graph2[node], do
if it is not visited and dist[it] > 0, then −
dist[it] := 0
insert it into q
insert it into visited
for each element it in graph1[node], do
if it is not visited and dist[it] > 1, then −
dist[it] := 1
insert it into q
insert it into visited
return ret
Example
Let us see the following implementation to get better understanding −
#include <bits/stdc++.h>
using namespace std;
const int N = 5e4 + 5;
class Solution {
public:
vector<int> graph1[N];
vector<int> graph2[N];
int minReorder(int n, vector<vector<int> >& e){
map<int, int> in;
for (auto& it : e) {
graph1[it[0]].push_back(it[1]);
graph2[it[1]].push_back(it[0]);
}
vector<int> dist(n, N + 10);
int ret = 0;
in[0] = 0;
dist[0] = 0;
queue<int> q;
q.push(0);
set<int> visited;
visited.insert(0);
while (!q.empty()) {
int node = q.front();
q.pop();
ret += dist[node];
for (auto& it : graph2[node]) {
if (!visited.count(it) && dist[it] > 0) {
dist[it] = 0;
q.push(it);
visited.insert(it);
}
}
for (auto& it : graph1[node]) {
if (!visited.count(it) && dist[it] > 1) {
dist[it] = 1;
q.push(it);
visited.insert(it);
}
}
}
return ret;
}
};
main(){
Solution ob;
vector<vector<int>> v = {{0,1},{1,3},{2,3},{4,0},{4,5}};
cout << (ob.minReorder(6,v));
}Input
6,{{0,1},{1,3},{2,3},{4,0},{4,5}}Output
3
321 Views
