Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Python Program to find the number of operations to pack several metal bars in a container
Suppose, we are given the tasks to transport several metal bars of different sizes. But the transportation container is short in length, it can contain bars of length 1 only. We are provided n number of bars, and their lengths are given to us in a list. So, to fit all the bars in the container; we have to cut and divide all the bars so they are of unit sizes. Further, we fit all the bars into the container that cost us one operation. We have to find the number of operations we have to perform on the bars.
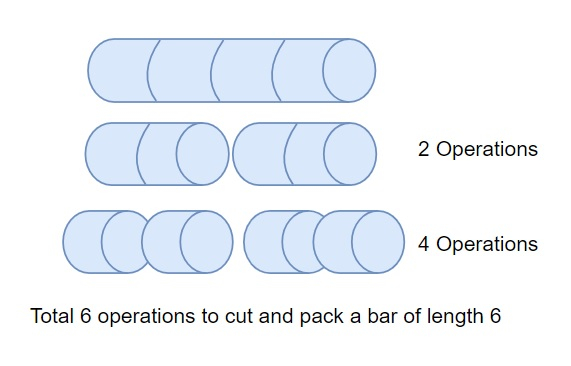
So, if the input is like input_arr = [6, 3, 7], then the output will be 22
To make the bar of size 6 into bars of size 1, we have to perform 10 operations.
To make the bar of size 3 into bars of size 1, we have to perform 4 operations.
To make the bar of size 7 into bars of size 1, we have to perform 8 operations.
To solve this, we will follow these steps −
Define a function prime_find() . This will take input_num
prime_check := a new list of size floor value of((input_num-1)/2) containing value True
for p_num in range 3 to the floor of square root of (input_num) +1, increase by 2, do
if prime_check[floor value of (p_num-3)/2] is non-zero, then
for each element in range floor value of (p_num ^ 2-3)/2 to p_num in prime_check, do
prime_check[element] := a new list of size (floor value of ((input_num-p_num ^2)/(2*p_num) + 1)) containing value False
for i in range 0 to floor value of (input_num - 1) / 2, do
- if prime_check[i] is True −
return a list containing values 2 + 2 * i + 3
- if prime_check[i] is True −
From the main function, do the following −
- prime_nums := prime_find(10^6 + 100)
- result := 0
- for each value in input_arr, do
- result := result + value
- f_list := a new list
- for each p_num in prime_nums, do
- while value mod p_num is same as 0, do
- insert p_num at the end of f_list
- value := floor value of (value / p_num)
- if p_num^2 > value, then
- if value > 1, then
- insert value at the end of f_list
- exit the loop
- if value > 1, then
- while value mod p_num is same as 0, do
- temp := 1
- for each p_num in f_list in reverse order, do
- result := result + temp
- temp := temp * p_num
- return result
Example
Let us see the following implementation to get better understanding −
from math import floor,sqrt def prime_find(input_num): prime_check = [True]*((input_num-1)//2) for p_num in range(3,floor(sqrt(input_num))+1,2): if prime_check[(p_num-3)//2]: prime_check[(p_num**2-3)//2::p_num] = [False] * ((input_num-p_num**2)//(2*p_num) + 1) return [2]+[2*i+3 for i in range((input_num - 1) // 2) if prime_check[i]] def solve(input_arr): prime_nums = prime_find(10**6+100) result = 0 for value in input_arr: result += value f_list = [] for p_num in prime_nums: while value % p_num == 0: f_list.append(p_num) value //= p_num if p_num**2 > value: if value > 1: f_list.append(value) break temp = 1 for p_num in f_list[-1::-1]: result += temp temp *= p_num return result if __name__ == "__main__": print(solve([6, 3, 7]))
Input
[6, 3, 7]
Output
22
132 Views
