Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Python Program for Product of unique prime factors of a number
In this article, we will learn about the solution to the problem statement given below −
Problem statement − Given a number n, we need to find the product of all of its unique prime factors available and return it.
For example,
Input: num = 11 Output: Product is 11 Explanation: Here, the input number is 11 having only 1 prime factor and it is 11. And hence their product is 11.
Approach 1
Using a for loop from i = 2 to n+1 check whether i is a factor of n & then check if i is the prime number itself, if yes then store product in product variable and continue this process until I become = n.
Example
def productPrimeFactors(n): product = 1 for i in range(2, n+1): if (n % i == 0): isPrime = 1 for j in range(2, int(i/2 + 1)): if (i % j == 0): isPrime = 0 break if (isPrime): product = product * i return product # main n = 18 print (productPrimeFactors(n))
Output
6
The scope of all the variables are shown in the image below −
Approach 2
While n is divisible by 2(even), print 2 and divide n by 2.
After step 1, n must become odd. Now start a for loop from i = 3 till the square root of n. While I divides n, print I and divide n by i. After I fail to divide n, increment I by 2 and continue the process.
If n is a prime number and is greater than 2, then n will not become 1 by above two steps. Hence print n if it is greater than 2.
Example
import math def productPrimeFactors(n): product = 1 # prime factor 2 if (n % 2 == 0): product *= 2 while (n%2 == 0): n = n/2 # n must be odd for i in range (3, int(math.sqrt(n)), 2): # While i divides n, print i and # divide n if (n % i == 0): product = product * i while (n%i == 0): n = n/i # n is a prime number greater than 2 if (n > 2): product = product * n return product # main() n = 8 print (int(productPrimeFactors(n)))
Output
2
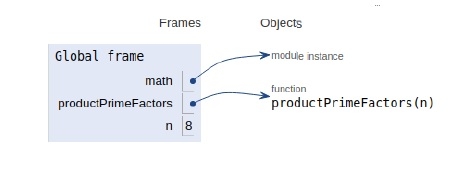
The scopes of the variables are mentioned in the image below −
Conclusion
In this article, we learned about the product of unique prime factors of a given number with a brute force approach and an efficient approach.
883 Views
