
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Python Program for Finding the vertex, focus and directrix of a parabola
In this article, we will learn about the solution to the problem statement given below −
Problem statement
The standard form of a parabola equation is y=ax^2+bx+c. Input the values of a, b and c, our task is to find the coordinates of the vertex, focus and the equation of the directrix.
The vertex of a parabola is the coordinate from which it takes the sharpest turn whereas y=a is the straight-line used to generate the curve.
A directrix a fixed-line used in describing a curve or surface.
Now let’s see the implementation −
Example
def findparabola(a, b, c):
print ("Vertex: (" , (-b / (2 * a)) , ", ",(((4 * a * c) - (b * b)) / (4 * a)) , ")" )
print ("Focus: (" , (-b / (2 * a)) , ", ", (((4 * a * c) -(b * b) + 1) / (4 * a)) , ")" )
print ("Directrix: y=", (int)(c - ((b * b) + 1) * 4 * a ))
# main()
a = 7
b = 5
c = 3
findparabola(a, b, c)
Output
Vertex: ( -0.35714285714285715 , 2.107142857142857 ) Focus: ( -0.35714285714285715 , 2.142857142857143 ) Directrix: y= -725
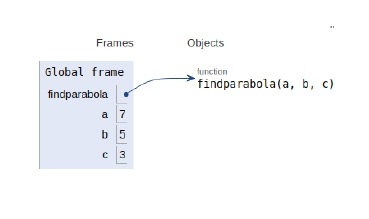
All the variables & the function are declared in the global scope as shown in the figure below.
Conclusion
In this article, we learned about finding the vertex, focus, and directrix of a parabola

Advertisements