
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Python Program for Extended Euclidean algorithms
In this article, we will learn about the solution to the problem statement given below.
Problem statement − Given two numbers we need to calculate gcd of those two numbers and display them.
GCD Greatest Common Divisor of two numbers is the largest number that can divide both of them. Here we follow the euclidean approach to compute the gcd i.e. to repeatedly divide the numbers and stop when the remainder becomes zero. Here we extend the algorithm based on previous values obtained in recursion.
Now let’s observe the solution in the implementation below −
Example
# extended Euclidean Algorithm
def gcdExtended(a, b, x, y):
# Base Case
if a == 0 :
x = 0
y = 1
return b
x1 = 1
y1 = 1 # storing the result
gcd = gcdExtended(b%a, a, x1, y1)
# Update x and y with previous calculated values
x = y1 - (b/a) * x1
y = x1
return gcd
x = 1
y = 1
a = 11
b = 15
g = gcdExtended(a, b, x, y)
print("gcd of ", a , "&" , b, " is = ", g)
Output
gcd of 11 & 15 is = 1
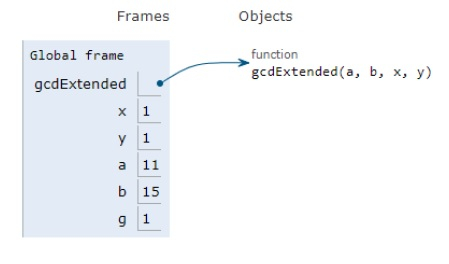
All the variables are declared in the local scope and their references are seen in the figure above.
Conclusion
In this article, we have learned about how we can make a Python Program for Extended Euclidean algorithms
