Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find tree level that has minimum sum in C++
Suppose we have a binary tree, the level of its root is 1, the level of its children is 2, and so on.We have to find the smallest level X such that the sum of all the values of nodes at level X is minimum. So if the tree is like −
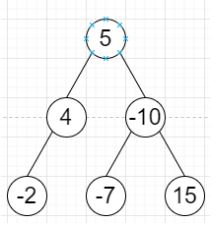
Output will be 2 as the sum is 4 – 10 = -6, which is minimum.
To solve this, we will follow these steps −
level := 1, sum := value of r, ansLevel := level, ansSum := sum
define a queue q, insert given node r into q
while q is not empty
capacity := size of q
increase level by 1, sum := 0
while capacity is not 0
node := front node from q, delete node from q
if right of node is valid, then sum := sum + value of right node, insert right
- node into q
if left of node is valid, then sum := sum + value of left node, insert left node into q
decrease capacity by 1
if ansSum < sum, then ansSum := sum, ansLevel := level
return ansLevel
Let us see the following implementation to get better understanding−
Example
#include <bits/stdc++.h>
using namespace std;
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = NULL;
right = NULL;
}
};
class Solution {
public:
int solve(TreeNode* r) {
int level = 1, sum = r->val;
int ansLevel = level, ansSum = sum;
queue <TreeNode*> q;
q.push(r);
while(!q.empty()){
int capacity = q.size();
level++;
sum = 0;
while(capacity--){
TreeNode* node = q.front();
q.pop();
if(node->right){
sum += node->right->val;
q.push(node->right);
}
if(node->left){
sum += node->left->val;
q.push(node->left);
}
}
if(ansSum>sum){
ansSum = sum;
ansLevel = level;
}
}
return ansLevel;
}
};
main(){
TreeNode *root = new TreeNode(5);
root->left = new TreeNode(4);
root->right = new TreeNode(-10);
root->left->right = new TreeNode(-2);
root->right->left = new TreeNode(-7);
root->right->right = new TreeNode(15);
Solution ob;
cout <<ob.solve(root);
}Input
TreeNode *root = new TreeNode(5); root->left = new TreeNode(4); root->right = new TreeNode(-10); root->left->right = new TreeNode(-2); root->right->left = new TreeNode(-7); root->right->right = new TreeNode(15);
Output
2
201 Views
To Continue Learning Please Login