Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find out the minimum value from sum of node values of sub-trees in Python
Suppose, we have a tree that has all of its nodes numbered as 1 to n. Each of the nodes contains an integer value. Now if we remove an edge from the tree, the difference in the sum of the node values of the two sub-trees has to be minimal. We have to find out and return the minimum difference between such sub-trees. The tree is given to us as a collection of edges, and the values of the nodes are also provided.
So, if the input is like n = 6, edge_list = [[1, 2], [1, 3], [2, 4], [3, 5], [3, 6]], values = [15, 25, 15, 55, 15, 65], then the output will be 0.
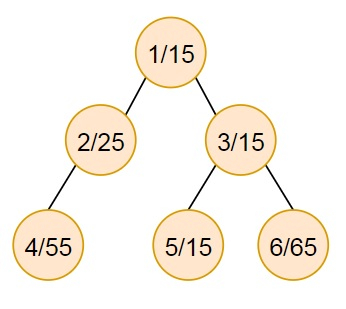
If edge (1,2) is removed, the sum of weights become 80, 110. Difference is 30.
If edge (1,3) is removed, the sum of weights become 95, 95. Difference is 0.
If edge (2,4) is removed, the sum of weights become 55, 135. Difference is 80.
If edge (3,5) is removed, the sum of weights become 15, 175. Difference is 160.
If edge (3,6) is removed, the sum of weights become 65, 125. Difference is 60.
So the minimum weight is 0.
To solve this, we will follow these steps −
- adj_list := a new list of size n containing empty lists
- for each edge in edge_list, do
- u := edge[0]
- v := edge[1]
- insert v-1 at the end of adj_list[u-1]
- insert u-1 at the end of adj_list[v-1]
- value_list := a new list of size n initialized with 0s
- not_visited := a new map of size i, where i is the number of non-empty lists in adj_list
- while not_visited is not empty, do
- for each i in not_visited, do
- value_list[i] := value_list[i] + values[i]
- if length of (adj_list[i]) is non-zero, then
- delete i from adj_list[adj_list[i, 0]]
- value_list[adj_list[i, 0]] := value_list[adj_list[i, 0]] + value_list[i]
- for each i in not_visited, do
- if len(adj_list[i]) and len(adj_list[adj_list[i, 0]]) == 1, then
- not_visited := a new list containing adj_list[i, 0]
- if len(adj_list[i]) and len(adj_list[adj_list[i, 0]]) == 1, then
- for each i in not_visited, do
- return_val := |sum(values) - 2 * value_list[0]|
- for i in range 1 to n, do
- decision_val := |sum(values) - 2 * value_list[i]|
- if decision_val < return_val, then
- return_val := decision_val
- return return_val
Example
Let us see the following implementation to get better understanding −
def solve(n, edge_list, values):
adj_list = [[] for i in range(n)]
for edge in edge_list:
u = edge[0]
v = edge[1]
adj_list[u-1].append(v-1)
adj_list[v-1].append(u-1)
value_list = [0] * n
not_visited = {i for i in range(n) if len(adj_list[i]) == 1}
while(len(not_visited)):
for i in not_visited:
value_list[i] += values[i]
if(len(adj_list[i])):
adj_list[adj_list[i][0]].remove(i)
value_list[adj_list[i][0]] += value_list[i]
not_visited = {adj_list[i][0] for i in not_visited if
len(adj_list[i]) and len(adj_list[adj_list[i][0]]) == 1}
return_val = abs(sum(values) - 2 * value_list[0])
for i in range(1, n):
decision_val = abs(sum(values) - 2 * value_list[i])
if decision_val < return_val:
return_val = decision_val
return return_val
print(solve(6, [[1, 2], [1, 3], [2, 4], [3, 5], [3, 6]], [10, 20, 10, 50, 10, 60]))Input
6, [[1, 2], [1, 3], [2, 4], [3, 5], [3, 6]], [10, 20, 10, 50, 10, 60]
Output
0
86 Views
