Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find out special types of subgraphs in a given graph in Python
Suppose we have a special type of graph that has two types of vertices that are named head and feet. The graph has only one head and there are k edges that connect the head to each of the feet. So, if we are given an undirected, unweighted graph; we shall have to find out these special types of graphs in the vertex disjoint subgraphs of the graph. Any two graphs are said to be vertex disjoint if they have no vertex in common.
So, if the input is like
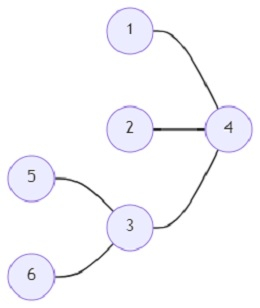
number of nodes (n) = 5, number of feet (t) = 2, then the output will be 5.
There can be 5 such special graphs that are vertex disjoint subgraphs of the given graph.
To solve this, we will follow these steps −
- G := a new list that contain n+1 empty lists
- for each item in edges, do
- s := item[0]
- d := item[1]
- insert d at the end of G[s]
- insert s at the end of G[d]
- visit := a new map
- for i in range 0 to n, do
- v := G[i]
- if size of v is same as 1, then
- s := v[0]
- if s not present in visit, then
- visit[s] := [i]
- otherwise,
- append i at the end of visit[s]
- otherwise when size of v is same as 0, then
- n := n - 1
- tmp := 0
- for each k in visit, do
- x := size of visit[k] -t
- if x > 0, then
- tmp := tmp + x
- return n - tmp
Example
Let us see the following implementation to get better understanding −
def solve(n, t, edges):
G = [[] for _ in range(n + 1)]
for item in edges:
s, d = map(int, item)
G[s].append(d)
G[d].append(s)
visit = {}
for i in range(n):
v = G[i]
if len(v) == 1:
s = v[0]
if s not in visit:
visit[s] = [i]
else: visit[s].append(i)
elif len(v) == 0:
n -= 1
tmp = 0
for k in visit:
x = len(visit[k])-t
if x > 0:
tmp += x
return n - tmp
print(solve(6, 2, [(1,4), (2,4), (3,4), (3,4), (5,3), (6,3)]))
Input
6, 2, [(1,4), (2,4), (3,4), (3,4), (5,3), (6,3)]
Output
5
Updated on: 06-Oct-2021
391 Views
Advertisements