Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find out if the graph is traversable by everybody in Python
Suppose, we are given a graph that contains n vertices numbered 0 to n - 1. The graph is undirected and each edge has a weight. The graph can have three types of weights and each weight signifies a particular task. There are two people that can traverse the graph, namely Jack and Casey. Jack can traverse the graph if an edge has weight 1, Casey can traverse the graph if it has weight 2, and both can traverse the graph if it has edge weight 3. We have to remove any edges necessary to make the graph traversable for both Jack and Casey. We return the number of edges to remove to make the graph traversable, or we return -1 if it cannot be made traversable.
So, if the input is like
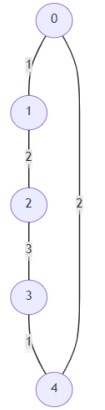
and n =5; then the output will be -1
The graph cannot be made traversable for both by removing an edge. So, the answer is -1.
To solve this, we will follow these steps −
Define a function find() . This will take val
if val is not same as root[val], then
root[val] := find(root[val])
return root[val]
Define a function union() . This will take val1, val2
val1:= find(val1)
val2 := find(val2)
if val1 is same as val2, then
return 0
root[val1] := val2
return 1
res := 0
edge1 := 0
edge2 := 0
root := a new list from range 0 to n + 1
for each edge (u, v), and its weight w in e, do
if u is same as 3, then
if union(v, w) is non-zero, then
edge1 := edge1 + 1
edge2 := edge2 + 1
otherwise,
res := res + 1
root0 := root[from index 0 to end]
for each edge (u, v), and its weight w in e, do
if u is same as 1, then
if union(v, w) is non-zero, then
edge1 := edge1 + 1
otherwise,
res := res + 1
root := root0
for each edge (u, v), and its weight w in e, do
if u is same as 2, then
if union(v, w) is non-zero, then
edge2 := edge2 + 1
otherwise,
res := res + 1
return res if edge1 is same as edge2 and n - 1
otherwise, return -1
Example
Let us see the following implementation to get better understanding
def solve(n, e):
def find(val):
if val != root[val]:
root[val] = find(root[val])
return root[val]
def union(val1, val2):
val1, val2 = find(val1), find(val2)
if val1 == val2: return 0
root[val1] = val2
return 1
res = edge1 = edge2 = 0
root = list(range(n + 1))
for u, v, w in e:
if u == 3:
if union(v, w):
edge1 += 1
edge2 += 1
else:
res += 1
root0 = root[:]
for u, v, w in e:
if u == 1:
if union(v, w):
edge1 += 1
else:
res += 1
root = root0
for u, v, w in e:
if u == 2:
if union(v, w):
edge2 += 1
else:
res += 1
return res if edge1 == edge2 == n - 1 else -1
print(solve(5, [(0,1,1),(1,2,2),(2,3,3),(3,4,1),(4,0,2)]))Input
Input: 5, [(0,1,1),(1,2,2),(2,3,3),(3,4,1),(4,0,2)]
Output
-1
127 Views
