Program to find out the number of boxes to be put into the godown in Python

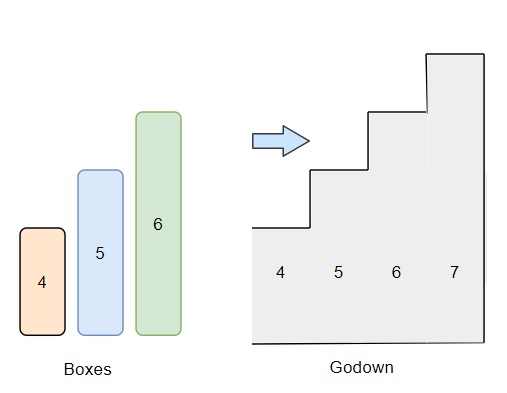
Suppose we have two arrays containing integers. One list contains the height of some unit width boxes and another array contains the height of rooms in the godown. The rooms are numbered 0...n, and the height of the rooms is provided in their respective indexes in the array godown. We have to find out the number of boxes that can be pushed into the godown. A few things have to be kept in mind:

• The boxes can't be put one on another.

• The order of the boxes can be changed.

• The boxes are put into the godown from left to right only.

If a box is taller than the height of the room, then the box along with all the boxes to its right cannot be pushed into the godown.

Problem Understanding

Let's understand this with an example. If the input is like boxes = [4,5,6], godown = [4, 5, 6, 7], then the output will be 1. Only one box can be inserted because the first room is of size 4 and the rest cannot be pushed into the godown since boxes have to be pushed through the first room first.

Algorithm Approach

To solve this problem, we follow these steps:

• Sort the boxes in ascending order (smallest first)

• Create a minimum height array that tracks the minimum room height from left to each position

• Use a greedy approach: try to place boxes from right to left in the godown

Solution Implementation

def solve(boxes, godown):
    # Sort boxes in ascending order
    boxes.sort()
    
    # Create minimum height array from left to right
    curmin = [godown[0]]
    cm = curmin[0]
    
    for i in range(1, len(godown)):
        cur = godown[i]
        if cur < cm:
            cm = cur
        curmin.append(cm)
    
    # Try placing boxes from right to left
    i, j = 0, len(godown) - 1
    count = 0
    
    while j >= 0 and i < len(boxes):
        if curmin[j] >= boxes[i]:
            i += 1
            count += 1
        j -= 1
    
    return count

# Test the function
boxes = [4, 5, 6]
godown = [4, 5, 6, 7]
result = solve(boxes, godown)
print(f"Number of boxes that can be placed: {result}")

Number of boxes that can be placed: 1

How It Works

Let's trace through the algorithm step by step:

def solve_with_trace(boxes, godown):
    print(f"Original boxes: {boxes}")
    print(f"Godown heights: {godown}")
    
    # Sort boxes
    boxes.sort()
    print(f"Sorted boxes: {boxes}")
    
    # Create minimum height array
    curmin = [godown[0]]
    cm = curmin[0]
    
    for i in range(1, len(godown)):
        cur = godown[i]
        if cur < cm:
            cm = cur
        curmin.append(cm)
    
    print(f"Minimum heights from left: {curmin}")
    
    # Place boxes
    i, j = 0, len(godown) - 1
    count = 0
    
    print("\nTrying to place boxes:")
    while j >= 0 and i < len(boxes):
        print(f"Position {j}, min_height: {curmin[j]}, box_height: {boxes[i]}")
        if curmin[j] >= boxes[i]:
            print(f"  ? Box {boxes[i]} can be placed at position {j}")
            i += 1
            count += 1
        else:
            print(f"  ? Box {boxes[i]} cannot be placed")
        j -= 1
    
    return count

# Trace the example
result = solve_with_trace([4, 5, 6], [4, 5, 6, 7])
print(f"\nFinal result: {result}")

Original boxes: [4, 5, 6]
Godown heights: [4, 5, 6, 7]
Sorted boxes: [4, 5, 6]
Minimum heights from left: [4, 4, 4, 4]

Trying to place boxes:
Position 3, min_height: 4, box_height: 4
  ? Box 4 can be placed at position 3
Position 2, min_height: 4, box_height: 5
  ? Box 5 cannot be placed
Position 1, min_height: 4, box_height: 5
  ? Box 5 cannot be placed
Position 0, min_height: 4, box_height: 5
  ? Box 5 cannot be placed

Final result: 1

Another Example

Let's test with a different configuration where more boxes can fit:

# Example where multiple boxes can fit
boxes2 = [2, 3, 4]
godown2 = [5, 4, 3, 2]
result2 = solve(boxes2, godown2)
print(f"Boxes: {boxes2}, Godown: {godown2}")
print(f"Number of boxes that can be placed: {result2}")

# Trace this example
print("\nDetailed trace:")
solve_with_trace([2, 3, 4], [5, 4, 3, 2])

Boxes: [2, 3, 4], Godown: [5, 4, 3, 2]
Number of boxes that can be placed: 3

Detailed trace:
Original boxes: [2, 3, 4]
Godown heights: [5, 4, 3, 2]
Sorted boxes: [2, 3, 4]
Minimum heights from left: [5, 4, 3, 2]

Trying to place boxes:
Position 3, min_height: 2, box_height: 2
  ? Box 2 can be placed at position 3
Position 2, min_height: 3, box_height: 3
  ? Box 3 can be placed at position 2
Position 1, min_height: 4, box_height: 4
  ? Box 4 can be placed at position 1
Position 0, min_height: 5, box_height: 4
  ? Box 4 can be placed at position 0

Final result: 3

Conclusion

This algorithm efficiently solves the godown box placement problem by sorting boxes and using a greedy approach. The key insight is that boxes must pass through all rooms from left to the target position, so we track minimum heights and place smaller boxes first in rightmost available positions.