Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find out an MST using Prim's algorithm in Python
Suppose we are given a graph and asked to find out the 'Minimum Spanning Tree' (MST) from that graph. An MST of a graph is a subset of a weighted graph where all the vertices are present and connected, and there exists no cycle in the subset. MST is called minimum because the total edge weight of the MST is the minimum possible from the graph. So, here we use Prim's MST algorithm and find out the total edge weight of the MST from a given graph.
So, if the input is like
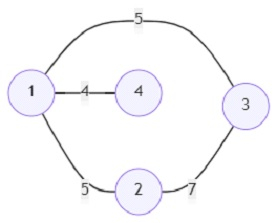
, number of vertices (n) is 4, and start vertex (s) = 3, then the output will be 14.
The MST from this graph will be this −
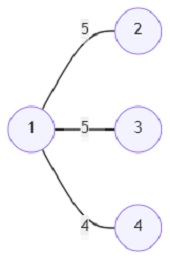
The total edge weight of this MST is 14.
To solve this, we will follow these steps −
- Define a function mst_find() . This will take G, s
- distance := a new list of size G initialized with value negative infinity
- distance[s] := 0
- itr := a new list of size G initialized with value False
- c := 0
- while True, do
- min_weight := infinity
- m_idx := -1
- for i in range 0 to size of G, do
- if itr[i] is same as False, then
- if distance[i] < min_weight, then
- min_weight := distance[i]
- m_idx := i
- if distance[i] < min_weight, then
- if itr[i] is same as False, then
- if m_idx is same as -1, then
- come out from the loop
- c := c + min_weight
- itr[m_idx] := True
- for each pair i, j in values of G[m_idx], do
- distance[i] := minimum of distance[i], j
- return c
- G := a new map containing n other maps
- for each item in edges, do
- u := item[0]
- v := item[1]
- w := item[2]
- u := u - 1
- v := v - 1
- min_weight = min(G[u, v], w)
- G[u, v] := min_weight
- G[v, u] := min_weight
- return mst_find(G, s)
Example
Let us see the following implementation to get better understanding −
def mst_find(G, s):
distance = [float("inf")] * len(G)
distance[s] = 0
itr = [False] * len(G)
c = 0
while True:
min_weight = float("inf")
m_idx = -1
for i in range(len(G)):
if itr[i] == False:
if distance[i] < min_weight:
min_weight = distance[i]
m_idx = i
if m_idx == -1:
break
c += min_weight
itr[m_idx] = True
for i, j in G[m_idx].items():
distance[i] = min(distance[i], j)
return c
def solve(n, edges, s):
G = {i: {} for i in range(n)}
for item in edges:
u = item[0]
v = item[1]
w = item[2]
u -= 1
v -= 1
try:
min_weight = min(G[u][v], w)
G[u][v] = min_weight
G[v][u] = min_weight
except KeyError:
G[u][v] = w
G[v][u] = w
return mst_find(G, s)
print(solve(4, [(1, 2, 5), (1, 3, 5), (2, 3, 7), (1, 4, 4)], 3))
Input
4, [(1, 2, 5), (1, 3, 5), (2, 3, 7), (1, 4, 4)], 3
Output
14
2K+ Views
