Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find minimum number of steps required to catch the opponent in C++
Suppose we have a list of tree edges in the form [u, v], this indicates there is an undirected edge between u and v. And we also have two values x and y. If we are at node x, and our opponent is at node y. In the first round, we move, then in the next round the opponent moves and so on. The opponent can select to not make a move in a round. We have to find the minimum number of rounds it we need to catch the opponent.
So, if the input is like edges = [[0, 1], [0, 2], [1, 3], [1, 4]], x = 0, y = 3, then the output will be 3, as at first, we move from node 0 to 1. Then opponent stays in the current node 3. Then we move to node 3.
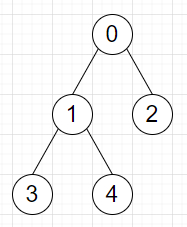
To solve this, we will follow these steps −
N := 1^5 + 5
Define an array visited of size: N and another array visited2 of size: N fill them with −1
create adjacency list graph for N nodes
for each edge it in edges list, do
insert it[v] at the end of graph[it[u]]
insert it[u] at the end of graph[it[v]]
Define one queue w
insert u into q
visited[u] := 0
while q is not empty, do −
node := first element of q
delete element from q
for each node it in graph[node]
if visited[it] is same as −1, then −
visited[it] := visited[node] + 1
insert it into q
insert v into q
ret := 0
visited2[v] := 0
while q is not empty), do −
node := first element of q
delete element from q
ret := maximum of ret and 2 * (visited[node])
for each node it in graph[node]
if visited2[it] is same as -1 and visited2[node] + 2 < visited[it], then −
visited2[it] := visited2[node] + 1
insert it into q
return ret
Let us see the following implementation to get better understanding −
Example
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int visited[N];
int visited2[N];
vector<int> graph[N];
class Solution {
public:
int solve(vector<vector<int>>& edges, int u, int v) {
memset(visited, −1, sizeof visited);
memset(visited2, −1, sizeof visited2);
for (int i = 0; i < N; i++)
graph[i].clear();
for (auto& it : edges) {
graph[it[0]].push_back(it[1]);
graph[it[1]].push_back(it[0]);
}
queue<int> q;
q.push(u);
visited[u] = 0;
while (!q.empty()) {
int node = q.front();
q.pop();
for (auto& it : graph[node]) {
if (visited[it] == −1) {
visited[it] = visited[node] + 1;
q.push(it);
}
}
}
q.push(v);
int ret = 0;
visited2[v] = 0;
while (!q.empty()) {
int node = q.front();
q.pop();
ret = max(ret, 2 * (visited[node]) − 1);
for (auto& it : graph[node]) {
if (visited2[it] == −1 && visited2[node] + 2 <
visited[it]) {
visited2[it] = visited2[node] + 1;
q.push(it);
}
}
}
return ret;
}
};
int solve(vector<vector<int>>& edges, int u, int v) {
return (new Solution())−>solve(edges, u, v);
}
int main(){
vector<vector<int>> edge = {{0, 1},{0, 2},{1, 3},{1, 4}};
int x = 0, y = 3;
cout << solve(edge, x, y);
}Input
[ [0, 1], [0, 2], [1, 3], [1, 4] ], 0, 3
Output
3
113 Views
