Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find maximum building height in Python
Suppose we have a value n and another list of pairs called restrictions. We want to build n new buildings in a city. But there are few restrictions. We can built in a line and buildings are labeled from 1 to n. The restrictions has two parameters, so restrictions[i] = (id_i, max_height_i) indicates id_i must have height less than or equal to max_height_i. The city restrictions on the heights of the new buildings are as follows −
The height of each building must be 0 or positive values.
First building height must be 0.
The difference between any two adjacent buildings height cannot exceed 1.
We have to find the maximum possible height of the tallest building.
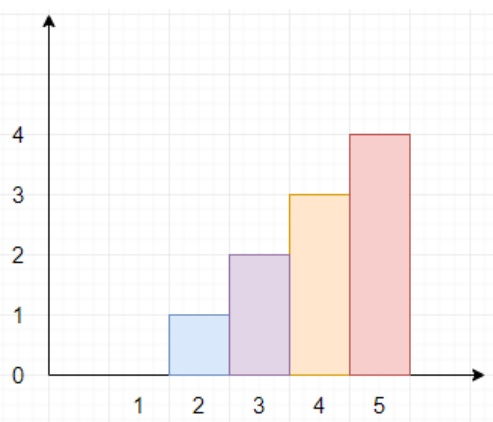
So, if the input is like n = 5, restrictions = [[2,1],[4,3]], then the output will be 4 because we have to find maximum possible height, so it can be 4 as shown in the diagram.
To solve this, we will follow these steps −
if restrictions is empty, then
return n-1
resi := sort the list restrictions based on id
k := 0
idx := 1
for each re in resi, do
re[1] := minimum of re[1] and (k+re[0]-idx)
k := re[1]
idx := re[0]
k := max height of last element in resi
idx := id of last element in resi
reverse the list resi
for each re in resi from first item onwards, do
re[1] := minimum of re[1] and (k-re[0]+idx)
k := re[1]
idx := re[0]
reverse the list resi
f := 0
idx := 1
res := 0
for each re in resi, do
ff := minimum of (f+re[0]-idx) and re[1]
res := maximum of res and quotient of (re[0] - idx + f + ff)/2
idx := re[0]
f := ff
return maximum of (f+n-idx) and res
Example
Let us see the following implementation to get better understanding
def solve(n, restrictions):
if not restrictions:
return n-1
resi = sorted(restrictions, key = lambda x:x[0])
k = 0
idx = 1
for re in resi:
re[1] = min(re[1], k+re[0]-idx)
k = re[1]
idx = re[0]
k = resi[-1][1]
idx = resi[-1][0]
resi.reverse()
for re in resi[1:]:
re[1] = min(re[1], k-re[0]+idx)
k = re[1]
idx = re[0]
resi.reverse()
f = 0
idx = 1
res = 0
for re in resi:
ff = min(f+re[0]-idx, re[1])
res = max(res, (re[0] - idx + f + ff) // 2)
idx = re[0]
f = ff
return max(f+n-idx,res)
n = 5
restrictions = [[2,1],[4,3]]
print(solve(n, restrictions))Input
5, [[2,1],[4,3]]
Output
4
544 Views
