Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find maximal network rank in Python
Suppose there are n cities and there are some roads connecting these cities. Each roads[i] = [u, v] indicates that there is a two-way road between cities u and v. Now consider network rank is the total number of directly connected roads to either city. When a road is directly connected to both cities, it is only counted once. And the maximal network rank of the network is the maximum network rank of all pairs of different cities. So, if we have different roads, we have to find the maximal network rank of the entire network.
So, if the input is like
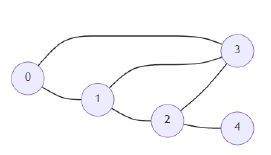
then the output will be 5 because there are five different ways to connect cities 1 and 2
To solve this, we will follow these steps −
- n := number of nodes
- s := a new set
- d := a map, if some key is not present then return 0 for it
- for each edge (x,y) in roads, do
- d[x] := d[x] + 1
- d[y] := d[y] + 1
- insert pair (x,y) into d
- ans := 0
- l := a new list from range 0 to n
- sort l based on node numbers in descending order
- threshold := minimum of d[l[0]] and d[l[1]]
- for i in range 0 to size of l - 1, do
- for j in range i+1 to size of l - 1, do
- if d[l[j]] < threshold, then
- come out from loop
- curr := d[l[i]] + d[l[j]]
- if (l[i],l[j]) is present in s or (l[j],l[i]) is present in s, then
- curr := curr - 1
- ans := maximum of ans and curr
- if d[l[j]] < threshold, then
- for j in range i+1 to size of l - 1, do
- return ans
Example
Let us see the following implementation to get better understanding −
from collections import defaultdict def solve(roads): nodes = set() s = set() d = defaultdict(int) for x,y in roads: nodes.update([x,y]) d[x]+=1 d[y]+=1 s.add((x,y)) ans = 0 n = len(nodes) l = list(range(n)) l.sort(key=lambda x:d[x], reverse = True) threshold = min(d[l[0]],d[l[1]]) for i in range(len(l)-1): for j in range(i+1,len(l)): if d[l[j]]<threshold: break curr = d[l[i]]+d[l[j]] if (l[i],l[j]) in s or (l[j],l[i]) in s: curr-=1 ans = max(ans,curr) return ans roads = [(0,1),(0,3),(1,2),(1,3),(2,3),(2,4)] print(solve(roads))
Input
[(0,1),(0,3),(1,2),(1,3),(2,3),(2,4)]
Output
5
325 Views
