Program to check whether we can color a tree where no adjacent nodes have the same color or not in python

Suppose we have a binary tree where the value of each node represents its color. There are at most 2 colors in a tree. We have to check whether it is possible to swap the colors of the nodes any number of times so that no two connected nodes have the same color.

So, if the input is like

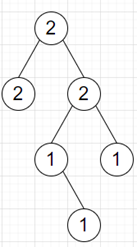
then the output will be True as we can get

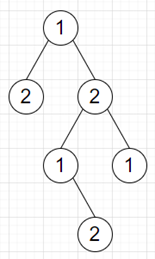
To solve this, we will follow these steps −

• colors := an empty map
• prop := an empty map
• Define a function dfs() . This will take node, and flag
• if node is null, then
  • return
• colors[value of node] := colors[value of node] + 1
• prop[flag] := prop[flag] + 1
• dfs(left of node, inverse of flag)
• dfs(right of node, inverse of flag)
• From the main method do the following:
• dfs(root, true)
• return true when all elements in colors and prop are same, otherwise false

Let us see the following implementation to get better understanding −

Example 

Live Demo

from collections import defaultdict
class TreeNode:
   def __init__(self, data, left = None, right = None):
      self.val = data
      self.left = left
      self.right = right

class Solution:
   def solve(self, root):
      colors = defaultdict(int)
      prop = defaultdict(int)

      def dfs(node, flag=True):
         if not node:
            return
         colors[node.val] += 1
         prop[flag] += 1
         dfs(node.left, not flag)
         dfs(node.right, not flag)

      dfs(root)
      return set(colors.values()) == set(prop.values())
     
ob = Solution()
root = TreeNode(2)
root.left = TreeNode(2)
root.right = TreeNode(2)
root.right.left = TreeNode(1)
root.right.right = TreeNode(1)
root.right.left.right = TreeNode(1)
print(ob.solve(root))

Input

root = TreeNode(2)
root.left = TreeNode(2)
root.right = TreeNode(2)
root.right.left = TreeNode(1)
root.right.right = TreeNode(1)
root.right.left.right = TreeNode(1)

Output

True

Arnab Chakraborty

Updated on: 02-Dec-2020

141 Views

Kickstart Your Career

Get certified by completing the course

Get Started