Principle of Mathematical Induction

Introduction

Mathematical induction involves principles which are a specific technique to prove theorems and statements in algebra which are expressed in the form of n; where n belongs to natural numbers. In mathematical induction any statement is proved for n=1 and then for any variable.

What is PMI?

Mathematical Induction can be described as a tool to prove any statement A(n) which can hold for natural numbers n=1, 2, 3, 4, 5......n. Mathematical Induction is based on some principles called the principle of mathematical induction (PMI).

In order to prove a result for a statement A(n), we can use the principles of mathematical induction. First we check if the statement holds for A(1). Then if the statement holds for A(1), we assume that it also holds for A(x), where x represents all the numbers till x, and applying the same hypothesis for A(x+1) is true. If A(x+1) holds then the statement A(x) becomes true for all natural numbers.

First Principle of Mathematical Induction

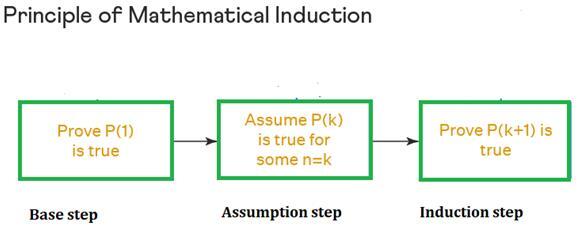
Let us look into the first principle of mathematical induction, and learn the steps used to prove the statement.

Let there be a statement A(n), where n belongs to a natural number.

Now let's prove that if the statement is true for n = 1, i.e., if A(1) is true or not.

If the statement is true for n=1, then we check the statement for n = x, where x is a natural number.

If the statement is true for n =x , then the equation will also be true for $\mathrm{P(x\:+\:1)}$. Therefore it can be established that the statement A(n) is true for $\mathrm{n\:\varepsilon\:N}$.

Solved Examples

Now let us look into an example based on the first PMI.

Let us take a statement that $\mathrm{n\:\varepsilon\:N}$

$$\mathrm{1\:+\:3\:+\:5\:+\:......\:+\:(2n\:-\:1)\:=\:n^{2}}$$

Answer −

Let the given statement A(n) be defined as $\mathrm{A(n)\:\colon\:1\:+\:3\:+\:5\:+\:......\:+\:(2n\:-\:1)\:=\:n^{2}}$ , for $\mathrm{n\:\varepsilon\:N}$

Base step − Note that A(1) is true

Because by putting n=1 we get

$\mathrm{1\:=\:1^{2}}$

Assumption step − Assume that A(x) is true for some $\mathrm{x\:\varepsilon\:N}$,

i.e.,$\mathrm{A(x)\:\colon\:1\:+\:3\:+\:5\:+\:......\:+\:(2n\:-\:1)\:=\:x^{2}}$

Induction step − In order to prove that P(x + 1) is true,

$\mathrm{A(x)\:\colon\:1\:+\:3\:+\:5\:+\:......\:+\:(2n\:-\:1)\:+\:(2n\:+\:1)\:=\:x^{2}\:+\:(2x\:+\:1)}$

$$\mathrm{=\:x^{2}\:+\:2x\:+\:1\:=\:(x\:+\:1)^{2}}$$

Thus, A(x + 1) is true when $\mathrm{x\:\varepsilon\:N}$.Hence A(x) is true for some $\mathrm{x\:\varepsilon\:N}$

Therefore, by the PMI, A(n) is true for all natural numbers.

Second Principle of Mathematical Induction

Now that we have learned about the first PMI let's understand what is the second PMI and where it can be used. Let us suppose we have a mathematical expression A(n) which is true for all n ∈ N . We know that the steps to prove are that if the expression holds for A(1), and then for any number x, then it must be true for P(x+1). The problem arises when we try to prove it after factoring in a composite number. For example, if we assume that A(29) is an expression that is true, and we have to use it to prove that P(30) also holds. If we factorize 30 as 30 = 2 × 15, the expression that A(29) is true cannot be used to prove that A(30) is also true.

Therefore we need a second principle to prove the induction. We assume an expression to be true and use it to prove that it is also true for the next number. The logic behind the second principle is that we assume the expression to be true for all the previous expressions and use it to prove the next expression is also true. In the second principle, we state the statement in terms of subsets of natural numbers. In many cases, we will use I=1 or I=0.

Let I be any integer and S is a subset of Y such that

• $\mathrm{I\:\varepsilon\:N}$

• For every $\mathrm{x\:\varepsilon\:Y}$ with $\mathrm{x\:\varepsilon\:Y}$ , If $\mathrm{\lbrace\:n\:\varepsilon\:Y\:|\:n\:\geq\:I\:\rbrace\:\subseteq\:S}$

Solved Examples

1) For a mathematical statement, $\mathrm{n\:=\:3a\:+\:5b}$, find which natural numbers (n) there exist non-negative integers a and b?

Answer −

Let the statement A(n) be true for $\mathrm{n\:=\:3a\:+\:5b}$, where $\mathrm{a\:\geq\:0\:or\:b\:\geq\:0}$

Let us see if the statement holds for a=0 and b=0.

$$\mathrm{n\:=\:3\:\times\:0\:+\:5\:\times\:0\:=\:0}$$

So it does not hold.

Now for example if $\mathrm{a\:>\:0}$ i.e. $\mathrm{a\:=\:1\:,\:b\:=\:0}$

Then $\mathrm{3\times\:1\:+\:5\times\:0\:=\:3}$

If $\mathrm{b\:>\:0}$ i.e., $\mathrm{b\:=\:1\:,\:a\:=\:0}$

Then $\mathrm{3\times\:0\:+\:5\times\:1\:=\:5}$

Therefore we can say that $\mathrm{3a\:+\:5b\:\geq\:3}$ if either a>0 or b>0

But we see that A(7) does not hold.

And if we have to prove if A(8) holds, we cannot use A(7) to prove it.

A(8) holds for a=1 and b=1,because $\mathrm{3\times\:1\:+\:5\times\:1\:=\:8}$

Thus, we can say that for each $\mathrm{n\:\varepsilon\:N\:with\:n\:\geq\:8}$ there exist non-negative integers a and b such that

$$\mathrm{n\:=\:3a\:+\:5b.}$$

Conclusion

Mathematical Induction is the concept of proving if a mathematical statement is true or not for all natural numbers n. Mathematical induction is generalized in the form of principles. Mathematical induction involves principles which are a specific technique to prove theorems and statements in algebra which are expressed in the form of n; where n belongs to natural numbers. In mathematical induction any statement is proved for n=1 and then for any variable. There are two principles in order to prove a statement:

Base step − In this step, we prove if A(1) is true.

Assumption step − In the second step, we assume A(x) to be true for a natural number x. Induction step: In the final step, we prove if $$\mathrm{A(x\:+\:1)} is true.

If all the steps are true, then we can say that "using the PMI, P(n) is true for all natural numbers."

FAQs

1. Name the steps in the first PMI?

The steps involved in the first PMI are Base step, Assumption step, and Induction step

2. What is the PMI in Matrices?

In matrices, the PMI is a concept of proving statements based on matrices.

3. What is mathematical induction?

A process of proving a mathematical statement with the help of steps based on established principles.

4. What is an inductive hypothesis in mathematical induction?

The second step i.e., assumption step in the PMI is called the inductive hypothesis

5. What is the difference between weak and strong induction?

In weak induction, we assume any statement that is true at the A(x) step, while in strong induction, the given statement A(n) is true for all the steps from the base to the A(x) step.