Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Optimize Water Distribution in a Village in Python
Suppose there are n houses in a village. We have to supply water for all the houses by building wells and laying pipes. For each house i, we can either build a well inside it, the building cost will be wells[i], or pipe in water from another well to it. The costs to lay pipes between houses are given by the array pipes, where each pipes[i] is [house1, house2, cost] represents the cost to connect house1 and house2 together using a pipe. These connections are bidirectional. We have to find the minimum total cost to supply water to all houses.
So, if the input is like n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]], then the output will be 3
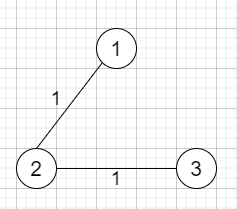
as from the above image shows the costs of connecting houses using pipes. The best strategy will be to build a well in the first house with cost 1 and connect the other houses to it with cost 2 so the total cost is 3.
To solve this, we will follow these steps −
Define a function find(). This will take a
if parent[a] is same as -1, then
return a
parent[a] := find(parent[a])
return parent[a]
Define a function union(). This will take a,b
parent_a := find(a)
parent_b := find(b)
if parent_a is same as parent_b, then
return True
parent[parent_b] := parent_a
return False
From the main method do the following −
parent := make a list of size n + 1, fill this with -1
counter := 0
for i in range 0 to size of well, do
insert [0, i+1, well[i]] at the end of pipes
counter := counter + 1
sort the pipes array based on the cost
cost := 0
for each i in pipes, do
source := i[0]
destination := i[1]
temp := i[2]
if union(source,destination) is false, then
cost := cost + temp
return cost
Let us see the following implementation to get better understanding −
Example
class Solution(object): def find(self, a): if self.parent[a] == -1: return a self.parent[a] = self.find(self.parent[a]) return self.parent[a] def union(self,a,b): parent_a = self.find(a) parent_b = self.find(b) if parent_a == parent_b: return True self.parent[parent_b] = parent_a return False def minCostToSupplyWater(self, n, well, pipes): self.parent = [-1 for i in range(n+1)] counter = 0 for i in range(len(well)): pipes.append([0,i+1,well[i]]) counter+=1 pipes = sorted(pipes,key=lambda v:v[2]) cost = 0 for i in pipes: #print(i) source = i[0] destination = i[1] temp = i[2] if not self.union(source,destination): cost+=temp return cost ob = Solution() print(ob.minCostToSupplyWater(3, [1,2,2], [[1,2,1],[2,3,1]]))
Input
3, [1,2,2], [[1,2,1],[2,3,1]]
Output
1
466 Views
