Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Number of Ways to Paint N × 3 Grid in C++
Suppose we have grid of size n x 3 and we want to paint each cell of the grid with exactly one of the three colors. The colors are Red, Yellow or Green. Now there is a constraint that is no two adjacent cells have the same color. We have n the number of rows of the grid. We have to find the number of ways we can paint this grid. The answer may be very large so return it modulo 10^9 + 7.
So, if the input is like 1, then the output will be 12
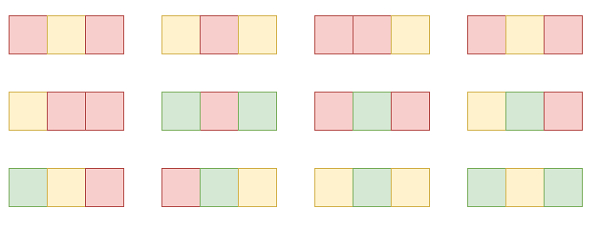
To solve this, we will follow these steps −
m = 1^9 + 7
Define a function add(), this will take a, b,
return ((a mod m) + (b mod m)) mod m
From the main method do the following −
a123 := 6, a121 = 6
for initialize i := 2, when i <= n, update (increase i by 1), do −
b121 := add(3 * a121, 2 * a123)
b123 := add(2 * a121, 2 * a123)
a121 := b121
a123 := b123
return add(a123, a121)
Let us see the following implementation to get better understanding −
Example
#include <bits/stdc++.h>
using namespace std;
typedef long long int lli;
const lli mod = 1e9 + 7;
class Solution {
public:
lli add(lli a, lli b){
return ((a % mod) + (b % mod)) % mod;
}
int numOfWays(int n){
lli a123 = 6, a121 = 6;
lli b123, b121;
for (int i = 2; i <= n; i++) {
b121 = add(3 * a121, 2 * a123);
b123 = add(2 * a121, 2 * a123);
a121 = b121;
a123 = b123;
}
return add(a123, a121);
}
};
main(){
Solution ob;
cout << (ob.numOfWays(3));
}Input
3
Output
246
239 Views
