Number of Possible Super Keys in DBMS

In database management systems (DBMS), super keys are an essential concept used to identify unique records in a table. A super key is a set of one or more than one attribute that can uniquely identify a record in a table.

In this article, we will explore the number of possible super keys in a database and their significance.

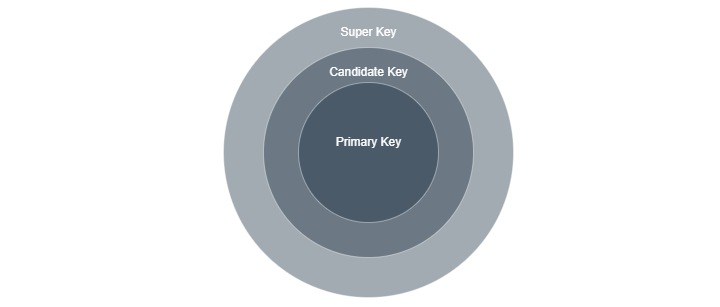
What is a Super Key?

A super key is a group of attributes in a table that can identify each row in that table uniquely. It's different from primary and candidate keys because only the smallest possible super keys can be chosen as primary or candidate keys. So, a primary or candidate key is a super key with no unnecessary attributes. All primary or candidate keys are super keys, but not all super keys are primary or candidate keys. The definition of a table states that all rows are unique, so the set of all attributes itself is a super key.

For example, if we have a table of students with columns: Student ID, Name, and Email. Here, the combination of Student ID and Name can form a super key. And also, Student ID, Name, and Email can also form a super key.

We will use here Inclusive-Exclusive various properties.

Counting Number of Possible Super Keys in DBMS

Example-1

Let's say we have a relation R with attributes {a1, a2, a3} and a1 is the candidate key. Then, any superset of a1 is the super key. Thus, we can have four possible super keys: {a1, a1 a2, a1 a3, a1 a2 a3}. In general, if we have ‘N’ attributes with one candidate key, then the number of possible superkeys is 2^(N – 1).

Example-2

Let's say we have a relation R with attributes {a1, a2, a3,…,an}. The maximum number of super keys is 2^(n) – 1. To be a super key, there should be at least one attribute present; the NULL set or the set with no attribute can't be a super key.

Example-3

Let's say we have a relation R with attributes {a1, a2, a3,…, an}, and the candidate key is “a1 a2 a3”. Following the previous formula, we have three attributes instead of one. So, here the number of possible super keys is 2^(N-3).

Example-4

Let's say we have a relation R with attributes {a1, a2, a3,…, an}, and the candidate keys are “a1”, “a2”. In this case, we have two different candidate keys instead of only one. We can use the following formula:

Super keys possible

= (super keys possible with candidate key A1) + (super keys possible with candidate key A2) – (common superkeys from both A1 and A2).

= = 2^(n-1) + 2^(n-1) - 2^(n-2)

Example-5

Let's say we have a relation R with attributes {a1, a2, a3,…, an}, and the candidate keys are “a1”, “a2 a3”. We can use the following formula:

= Super keys of (a1) + Super keys of (a2 a3) – Super keys of (a1 a2 a3).

= 2^(n - 1) + 2^(n - 2) - 2^(n - 3)

Example-6

Let's say we have a relation R with attributes {a1, a2, a3,…, an}, and the candidate keys are “a1 a2”, “a3 a4”. We can use the following formula:

= Super keys of(a1 a2) + Super keys of(a3 a4) – Super keys of(a1 a2 a3 a4).

= 2^(n - 2) + 2^(n - 2) - 2^(n - 4)

Example-7

Let's say we have a relation R with attributes {a1, a2, a3,…, an}, and the candidate keys are “a1 a2”, “a1 a3”. We can use the following formula:

= Super keys of (a1 a2) + Super keys of (a1 a3) – Super keys of(a1 a2 a3).

= 2^(n - 2) + 2^(n - 2) - 2^(n - 3)

Example-8

Suppose there is a Relation R with attributes {a1, a2, a3,…,an}. If the candidate keys are “a1”, “a2”, and “a3”, how many super keys are possible?

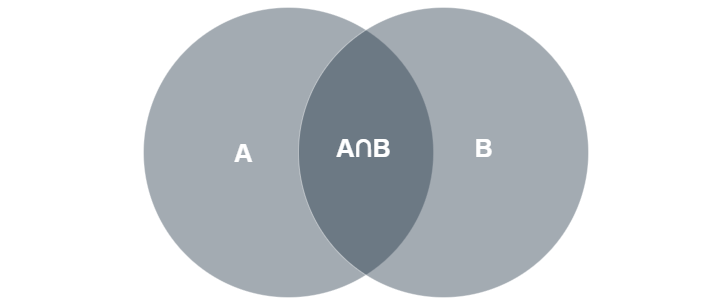
To find out the number of super keys, we can use a formula which is shown in the diagram below. We just need to plug in the number of attributes in the relation (n), and the number of candidate keys we have.

The formula is

|A1 ∪ A2 ∪ A3| = |A1| + |A2| + |A3| – |A1 ∩ A2| – |A1 ∩ A3| – |A2 ∩ A3| + |A1 ∩ A2 ∩ A3|

= (super keys possible with candidate key A1) + (super keys possible with candidate key A2) + (super keys possible with candidate key A3) – (common super keys from both A1 and A2) – (common super keys from both A1 and A3) – (common super keys from both A2 and A3) + (common super keys from both A1, A2, and A3)

= 2^(n-1) + 2^(n-1) + 2^(n-1) – 2^(n-2) – 2^(n-2) – 2^(n-2) + 2^(n-3)

Example-9

Let's say there is a relation R (A, B, C, D, E, F, G, H) and the set of functional dependencies are CH → G, A → BC, B → CFH, and E → A, F → EG. How many possible super keys are present?

First, we need to find out the candidate keys, which are AD, BD, ED, and FD. Then we need to find the possible super keys due to a single candidate key, a combination of two candidate keys, three candidate keys, and all candidate keys. After applying the inclusion-exclusion principle, we can find the number of super keys, which is 120.

Example-10

Let's say there is a relation R with attributes {a1, a2, a3…an} and {a1a2a3…ak} as the candidate key where k<=n. How many super keys are possible?

The possible number of super keys is 2^(n-k).

Example-11

Let's say there is a relation R with attributes {a1, a2, a3…an} such that any k of the attributes at a time determines all other attributes. We need to find the value of k such that the number of candidate keys in the relation will be maximum.

Any k attributes at a time constitute one candidate key. These k attributes are randomly chosen from the n attributes. So for some k, the possible number of candidate keys is nCk, which is n!/(n-k)!k!. For the number of candidate keys to be maximum, k must be ⌊n/2⌋ so that nCk is the maximum for that value.