Nth Catalan Number in Python Program

In this article, we will learn about calculating the nth Catalan number.

Catalan numbers are a sequence of natural numbers that are defined by the recursive formula −

$$c_{0} = 1\;and\; c_{n+1} = \displaystyle\sum\limits_{i=0}^nc_{i} c_{n-i}\; for n\geq 0 ;$$

The first few Catalan numbers for n = 0, 1, 2, 3, … are 1, 1, 2, 5, 14, 42, 132, 429,...................

Catalan numbers can be obtained both by recursion and dynamic programming.

So let’s see their implementation.

Approach 1: Recursion Method

Example

 Live Demo

Approach 1: Recursion Method

# A recursive solution
def catalan(n):
   #negative value
   if n <=1 :
      return 1
   # Catalan(n) = catalan(i)*catalan(n-i-1)
   res = 0
   for i in range(n):
      res += catalan(i) * catalan(n-i-1)
   return res
# main
for i in range(6):
   print (catalan(i))

Output

1
1
2
5
14
42

The scope of all the variables and recursive calls are shown below.

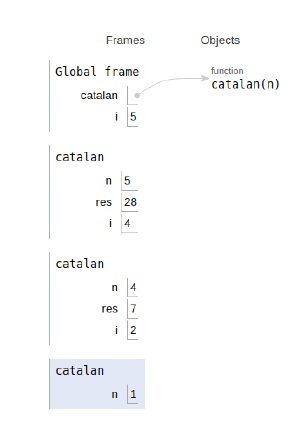
Approach 2: Dynamic Programming Method

Example

# using dynamic programming
def catalan(n):
   if (n == 0 or n == 1):
      return 1
   # divide table
   catalan = [0 for i in range(n + 1)]
   # Initialization
   catalan[0] = 1
   catalan[1] = 1
   # recursion
   for i in range(2, n + 1):
      catalan[i] = 0
      for j in range(i):
         catalan[i] = catalan[i] + catalan[j] * catalan[i-j-1]
   return catalan[n]
# main
for i in range (6):
   print (catalan(i),end=" ")

Output

1
1
2
5
14
42

The scope of all the variables and recursive calls are shown below.

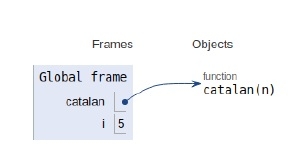
Conclusion

In this article, we learned about the method of generating the nth Catalan number