N-th Fibonacci number in Python Program

In this article, we will compute nth Fibonacci number.

A fibbonacci number is defined by the recurrance relation given below:

Fn = Fn-1 + Fn-2

With F₀ = 0 and F₁ = 1.

First few fibbonacci numbers are 0,1,1,2,3,5,8,13,..................

We can compute the Fibonacci numbers using the method of recursion and dynamic programming.

Now let’s see the implementation in the form of Python script

Approach 1: Recursion Method

Example

 Live Demo

#recursive approach
def Fibonacci(n):
   if n<0:
      print("Fibbonacci can't be computed")
   # First Fibonacci number
   elif n==1:
      return 0
   # Second Fibonacci number
   elif n==2:
      return 1
   else:
      return Fibonacci(n-1)+Fibonacci(n-2)
# main
n=10
print(Fibonacci(n))

Output

34

The scope of all the variables declared is shown below

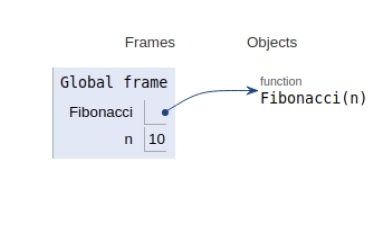
Approach 2: Dynamic Programming Method

Example

 Live Demo

#dynamic approach
Fib_Array = [0,1]
def fibonacci(n):
   if n<0:
      print("Fibbonacci can't be computed")
   elif n<=len(Fib_Array):
      return Fib_Array[n-1]
   else:
      temp = fibonacci(n-1)+fibonacci(n-2)
      Fib_Array.append(temp)
      return temp
# Driver Program
n=10
print(fibonacci(n))

Output

34

The scope of all the variables declared is shown below

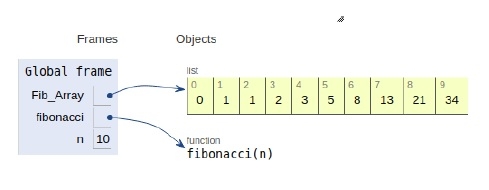
Conclusion

In this article, we learned about computation of nth Fibonacci number using recursion and dynamic programming approach.