Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Mutual Inductance with Dot Convention
When the EMF is induced by self and mutual inductance occur simultaneously, the relative polarities of these two induced EMFs must be determined before making any circuit calculations. The induced EMF in a coil due to mutual inductance may either aid or oppose the induced EMF due to self-inductance depending upon the sense of the windings and the directions of the currents in the coils.
Dot Notation or Dot Rule
The dot rule or dot convention may be stated as follows −
If both currents enter the dotted ends of the coupled coils or if both currents enter undotted ends, then the sign of mutual inductance (M) will be same as the signs of the self-inductance (L).
If one current enters a dotted end and the other enters at the un-dotted end, the sign of the mutual inductance (M) will be opposite to that of the self-inductance (L).
Explanation
If the two currents flow into each dot or out of each dot, the mutual inductance (M) will be positive. On the other hand, if one current flows into a dotted end and the other leaves the dotted end, then the mutual inductance (M) will be negative.
Consider the following circuit examples −
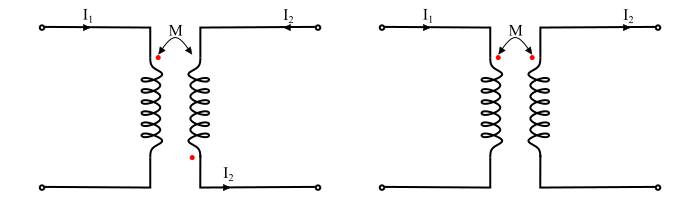
The mutual inductance (M) is positive because both the currents $I_{1}$ and $I_{2}$ flow into dots.
The M is positive because both the currents $I_{1}$ and $I_{2}$ flow out of the dots.
The M is negative since the current $I_{1}$ flows into the dot whereas the current $I_{2}$ flows out of the dot.
Circuit Equations for Coupled Inductors
The following circuit examples illustrate the writing of circuit equations for the coupled circuits.
Circuit 1
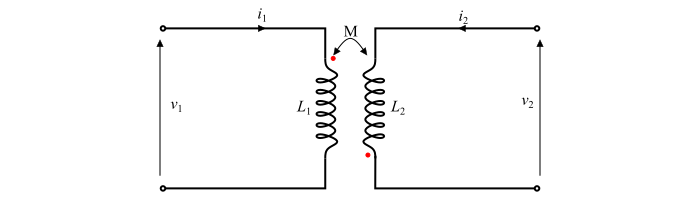
Consider a coupled circuit consisting of two inductors $L_{1}$ and $L_{2}$. Let $V_{1}$ and $V_{2}$ are the voltages being applied to respective inductors. Each of the two currents $I_{1}$ and $I_{2}$ are assumed to enter the dotted ends. Therefore, the sign of the mutual inductance (M) being positive.
By applying KVL, the voltage equations can be written as,
$$\mathrm{V_{1}=L_{1}\frac{di_{1}}{dt}+M\frac{di_{2}}{dt}\:\:\:\:\:\:...(1)}$$
$$\mathrm{V_{2}=L_{2}\frac{di_{2}}{dt}+M\frac{di_{1}}{dt}\:\:\:\:\:\:...(2)}$$
Circuit 2
Consider a coupled circuit consisting of two inductors $L_{1}$ and $L_{2}$. Let $V_{1}$ and $V_{2}$ are the voltages being applied to respective inductors. The current $I_{1}$ is assumed to enter the dotted terminal whereas the current $I_{2}$ is leaving the dotted terminal. Therefore, the sign of the mutual inductance (M) being negative.
9K+ Views
