Concepts & Classification

In this chapter, we will discuss various concepts and classification of Modelling.

Models & Events

Following are the basic concepts of Modelling & Simulation.

Object is an entity which exists in the real world to study the behavior of a model.
Base Model is a hypothetical explanation of object properties and its behavior, which is valid across the model.
System is the articulate object under definite conditions, which exists in the real world.
Experimental Frame is used to study a system in the real world, such as experimental conditions, aspects, objectives, etc. Basic Experimental Frame consists of two sets of variables − the Frame Input Variables & the Frame Output Variables, which matches the system or model terminals. The Frame input variable is responsible for matching the inputs applied to the system or a model. The Frame output variable is responsible for matching the output values to the system or a model.
Lumped Model is an exact explanation of a system which follows the specified conditions of a given Experimental Frame.
Verification is the process of comparing two or more items to ensure their accuracy. In Modelling & Simulation, verification can be done by comparing the consistency of a simulation program and the lumped model to ensure their performance. There are various ways to perform validation process, which we will cover in a separate chapter.
Validation is the process of comparing two results. In Modelling & Simulation, validation is performed by comparing experiment measurements with the simulation results within the context of an Experimental Frame. The model is invalid, if the results mismatch. There are various ways to perform validation process, which we will cover in separate chapter.

System State Variables

The system state variables are a set of data, required to define the internal process within the system at a given point of time.

In a discrete-event model, the system state variables remain constant over intervals of time and the values change at defined points called event times.
In continuous-event model, the system state variables are defined by differential equation results whose value changes continuously over time.

Following are some of the system state variables −

Entities & Attributes − An entity represents an object whose value can be static or dynamic, depending upon the process with other entities. Attributes are the local values used by the entity.
Resources − A resource is an entity that provides service to one or more dynamic entities at a time. The dynamic entity can request one or more units of a resource; if accepted then the entity can use the resource and release when completed. If rejected, the entity can join a queue.
Lists − Lists are used to represent the queues used by the entities and resources. There are various possibilities of queues such as LIFO, FIFO, etc. depending upon the process.
Delay − It is an indefinite duration that is caused by some combination of system conditions.

Classification of Models

A system can be classified into the following categories.

Discrete-Event Simulation Model − In this model, the state variable values change only at some discrete points in time where the events occur. Events will only occur at the defined activity time and delays.
Stochastic vs. Deterministic Systems − Stochastic systems are not affected by randomness and their output is not a random variable, whereas deterministic systems are affected by randomness and their output is a random variable.
Static vs. Dynamic Simulation − Static simulation include models which are not affected with time. For example: Monte Carlo Model. Dynamic Simulation include models which are affected with time.
Discrete vs. Continuous Systems − Discrete system is affected by the state variable changes at a discrete point of time. Its behavior is depicted in the following graphical representation.

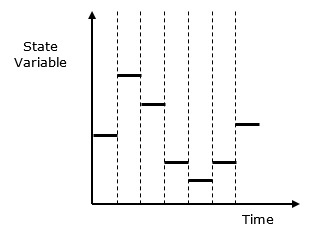
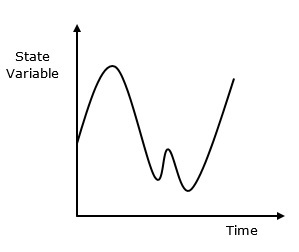
Continuous system is affected by the state variable, which changes continuously as a function with time. Its behavior is depicted in the following graphical representation.

Modelling Process

Modelling process includes the following steps.

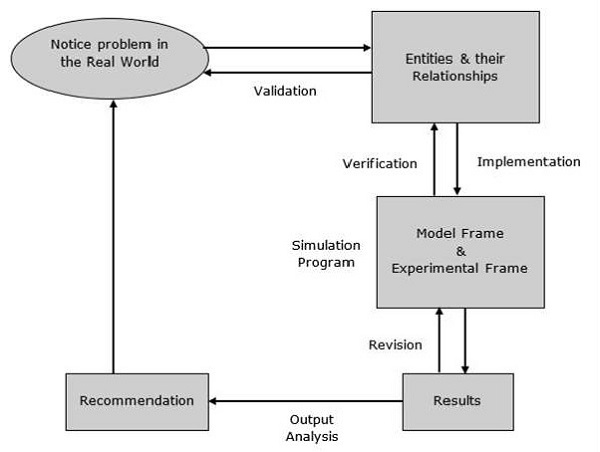
Step 1 − Examine the problem. In this stage, we must understand the problem and choose its classification accordingly, such as deterministic or stochastic.

Step 2 − Design a model. In this stage, we have to perform the following simple tasks which help us design a model −

Collect data as per the system behavior and future requirements.
Analyze the system features, its assumptions and necessary actions to be taken to make the model successful.
Determine the variable names, functions, its units, relationships, and their applications used in the model.
Solve the model using a suitable technique and verify the result using verification methods. Next, validate the result.
Prepare a report which includes results, interpretations, conclusion, and suggestions.

Step 3 − Provide recommendations after completing the entire process related to the model. It includes investment, resources, algorithms, techniques, etc.