Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Minimum Time to Collect All Apples in a Tree in C++
Suppose we have an undirected tree consisting of n vertices and these are numbered from 0 to n-1, which has some apples in their vertices. We spend 1 second to walk over one edge of the tree. We have to find the minimum time in seconds we have to spend in order to collect all apples in the tree starting at vertex 0 and coming back to this vertex.
Here the edges of the undirected tree are given in the array edges, where edges[i] = [from_i, to_i] this means that exists an edge connecting the vertices from_i and to_i. Additionally, there is another array has apple, where hasApple[i] = true means that vertex i has an apple, otherwise, it does not have any apple.
So, if the input is like n = 7 and edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], and has apple = [false, false, true, false, true, true, false], then the output will be 8,
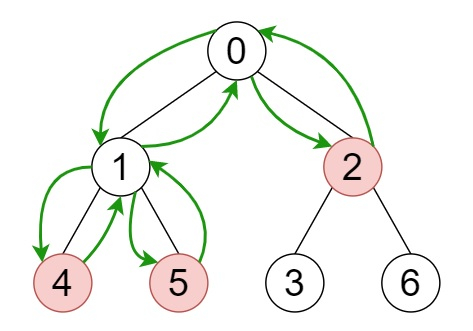
as from the above image we can see the tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
To solve this, we will follow these steps −
Define one set visited
Define a function dfs(), this will take node, par, an array a, an array graph[],
temp := 0
for each element x in graph[node] −
if x is same as par, then −
Ignore following part, skip to the next iteration
temp := temp + dfs(x, node, a, graph)
ret := ret + temp * 2
return true when a[node] + temp > 0, otherwise 0
From the main method do the following −
ret := 0
Define an array of n lists called graph
for initialize i := 0, when i < size of e, update (increase i by 1), do −
insert e[i, 1] at the end of graph[e[i, 0]]
insert e[i, 0] at the end of graph[e[i, 1]]
dfs(0, -1, a, graph)
return ret
Example
Let us see the following implementation to get better understanding −
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6;
class Solution {
public:
set<int> visited;
int ret;
int dfs(int node, int par, vector<bool>& a, vector<int> graph[]){
int temp = 0;
for (int x : graph[node]) {
if (x == par)
continue;
temp += dfs(x, node, a, graph);
}
ret += temp * 2;
return a[node] + temp > 0;
}
int minTime(int n, vector<vector<int> >& e, vector<bool>& a){
ret = 0;
vector<int> graph[n];
for (int i = 0; i < e.size(); i++) {
graph[e[i][0]].push_back(e[i][1]);
graph[e[i][1]].push_back(e[i][0]);
}
dfs(0, -1, a, graph);
return ret;
}
};
main(){
Solution ob;
vector<vector<int>> v = {{0,1},{0,2},{1,4},{1,5},{2,3},{2,6}};
vector<bool> v1 = {false,false,true,false,true,true,false};
cout << (ob.minTime(7,v, v1));
}Input
7, {{0,1},{0,2},{1,4},{1,5},{2,3},{2,6}},
{false,false,true,false,true,true,false}Output
8
384 Views
