Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Mean-Variance criterion for defining efficient and inefficient assets
Mean-Variance Analysis
Mean-Variance Analysis is a process that investors utilize to make investment decisions based on their risk tolerance. Investors actually consider the potential variance given by the volatility of returns produced by an asset in the market against the required expected returns of that asset. The mean-variance analysis looks into the average variance in the required expected return from an investment.
The mean-variance analysis is a part of Modern Portfolio Theory (MPT) which is based on the assumption that investors tend to make rational decisions when they possess enough information. The theory also relies on the fact that investors enter the market to simultaneously maximize their returns while avoiding unnecessary risk.
Investors will generally prefer the asset with lower variance from similar assets when allowed to choose.
Main Components of Mean-Variance Analysis
The mean-variance analysis is comprised of two main components −
- Variance
- Expected Return
Variance
By variance, we measure the distance or spread of the data in a data set from the mean, or average. A large variance shows that the numbers are widely spread out while a small variance represents a small variance of numbers from the mean.
The variance may also be equal to zero, which shows no deviation has occurred from the mean. During the analysis of an investment portfolio, variance shows how the returns are spread out during a given period of time.
Expected Return
The expected return is the estimated return security is expected to produce. It is not quite guaranteed as most of the concerns are made depending on the historical data.
Investors usually choose the security out of many that have a lower variance. If two securities show the same variance, the one with the higher expected return will be preferred by the investors.
Markowitz Efficient Set
The Markowitz Efficient Set is a portfolio with maximum returns for a given level of risk based on mean-variance portfolio construction. The efficient solution for a given set of mean-variance parameters which is a given riskless asset and a given risky basket of assets can be plotted on the graph on what is called the Markowitz efficient frontier.
The efficient set is plotted with returns on the Y-axis and risk or the standard deviation on the X-axis. The efficient set is on the line (frontier line) where the higher risk is positively correlated with given increasing returns, which means "higher risk, higher returns.” The best way to build a portfolio is to get the highest returns at a chosen level of risk.
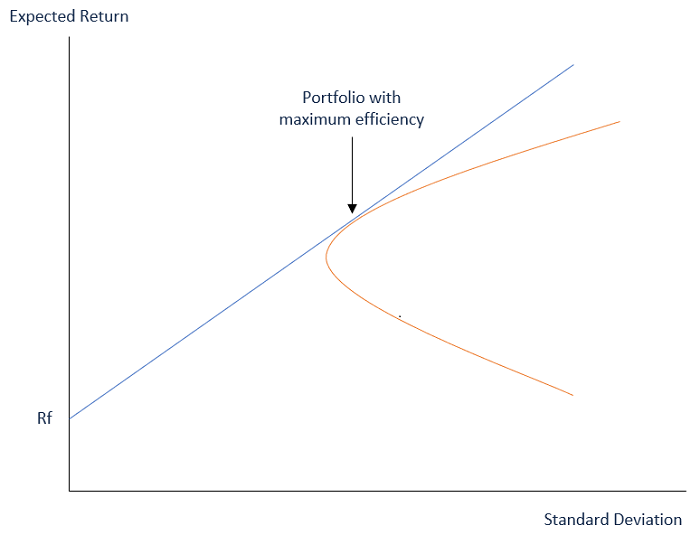
All individuals do not invest in the same securities, as their risk tolerance levels are different. Moreover, investors cannot assume that there is a guarantee of higher returns if they invest in riskier securities. In fact, the set of portfolio becomes inefficient if returns go down at greater levels of risk. At the core of Markowitz efficient set theory is diversification, which lowers portfolio risk.
As different combinations of assets provide different levels of return, the Markowitz efficient set is meant to show the most fruitful combination of the assets which will maximize returns at a chosen risk level. The Markowitz efficient set indicates to investors how returns vary depending on the amount of risk assumed.
619 Views
