- Trending Categories
Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Max Points on a Line in C++
Suppose we have a 2D plane. We have to find the maximum number of points that reside on the same straight line. So if the points are like −
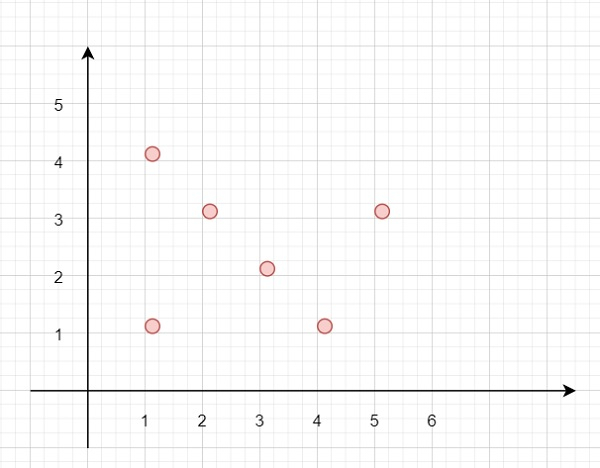
Then there are 4 points
To solve this, we will follow these steps −
n := number of points, if n < 3, then return n
ans := 2
for i in range 1 to n – 1
count := 0
take two points from index i and i – 1, these are p1, p2
if p1 and p2 points are same, then
for j in range 0 to n – 1
if points[j].x = p1.x and points[j].y = p1.y, then increase count by 1
otherwise −
for j in range 0 to n – 1
p3 := point from index j
if p3.y – p2.y * p2.x – p1.x = p2.y – p1.y * p3.x – p2.x, then increase count by 1
ans := max of ans and count
return ans
Example
Let us see the following implementation to get a better understanding −
#include <bits/stdc++.h>
using namespace std;
typedef long long int lli;
class Solution {
public:
int maxPoints(vector<vector<int>>& points) {
int n = points.size();
if(n<3)return n;
int ans = 2;
for(int i = 1;i<n;i++){
int count = 0;
lli x1 = points[i-1][0];
lli x2 = points[i][0];
lli y1 = points[i-1][1];
lli y2 = points[i][1];
if(x1 == x2 && y1 == y2){
for(int j =0;j<n;j++){
if(points[j][0] ==x1 && points[j][1] == y1)count++;
}
} else {
for(int j =0;j<n;j++){
int x3 = points[j][0];
int y3 = points[j][1];
if((y3-y2)*(x2-x1) == (y2-y1)*(x3-x2))count++ ;
}
}
ans = max(ans, count);
}
return ans;
}
};
main(){
Solution ob;
vector<vector<int>> v = {{1,1},{3,2},{5,3},{4,1},{2,3},{1,4}};
cout << (ob.maxPoints(v));
}Input
[{1,1},{3,2},{5,3},{4,1},{2,3},{1,5}]Output
4
Updated on: 26-May-2020
305 Views
Advertisements