Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Magnetic Circuit with Air Gap: Explanation and Examples
B-H Curve or Magnetisation Curve
The B-H curve or magnetisation curve is the graph plotted between magnetic flux density (B) and magnetising force (H). The B-H curve indicates the manner in which the magnetic flux density varies with the change in magnetising force.
The following figure shows the general shape of B-H curve of a magnetic material. The nonlinearity of the curve shows that the relative permeability $μ_{r}$ of a magnetic material is not constant but varies depending upon the magnetic flux density.
Magnetic Hysteresis
The phenomenon of lagging of magnetic flux density (B) behind the magnetising force (H) in a magnetic material subjected to the cycle of magnetisation (i.e., it is magnetised first in one direction and then in the other) is called as magnetic hysteresis.
Hysteresis Loop
Consider a coil of N turns wound on an un-magnetised iron bar AB (see the figure). The magnetising force (H = NI/l) produced by the coil can be changed by varying the current through the coil. It can be seen that when the iron bar is subjected to one complete cycle of magnetisation, the resultant B-H curve traces a loop abcdefa called as hysteresis loop.
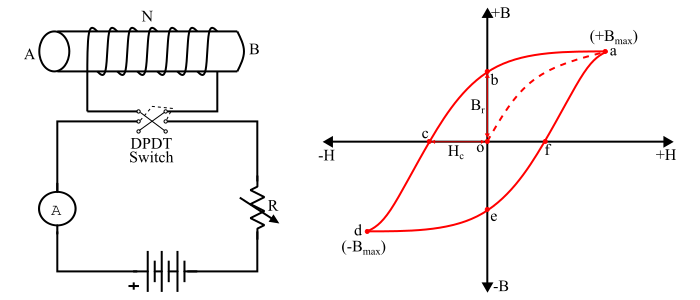
Explanation
When the current in the coil is zero, the H is zero and hence B in the iron bar is zero. When H is increased by increasing the coil current, the magnetic flux density also increases until the point of maximum magnetic flux density $\mathit{(+B_{max})}$ is reached. At this point, the material is saturated and beyond this point, the magnetic flux density will not increase regardless of any increase of magnetising force (H). For this, the B-H curve follows the path oa (see the hysteresis loop).
Now, if the H is gradually decreased by decreasing the coil current, it is found that the magnetic flux density does not decrease along the path oa but follows the path ab. At point b, the magnetising force is zero but magnetic flux density in the material has a finite value (equal to ob) called residual flux density $\mathit{(+B_{r})}$. The ability of retaining residual magnetism by a magnetic material is called as retentivity of the material.
In order to demagnetise the iron bar i.e. to remove the residual magnetism (ob), the magnetising force is reversed by reversing the coil current. When H is gradually increased in the reversed direction, the B-H curve follows the path bc so that when H = oc, the residual magnetism is zero. The values of H = oc required to completely remove the residual magnetism is known as coercive force $(H_{c})$.
Now, if H is further increased in reverse direction, the material again saturates in the reverse direction (point d). Reducing H to zero and then increasing it in the positive direction traces the curve defa. Therefore, when an iron bar is subjected to one complete cycle of magnetisation, the B-H curve traces a closed loop abcdefa called hysteresis loop.
Importance of Hysteresis Loop
The shape and size of the hysteresis loop depends upon the nature of the material. The choice of a magnetic material for a particular application depends upon the shape and size of the hysteresis loop.
Consider the following cases of hysteresis loop to understand it importance −
The smaller the area of the hysteresis loop of a magnetic material, the less is the hysteresis loss (e.g. silicon steel). Therefore, the silicon steel is widely used for making cores of transformer and rotating electric machines which are subjected to rapid reversals of magnetisation.
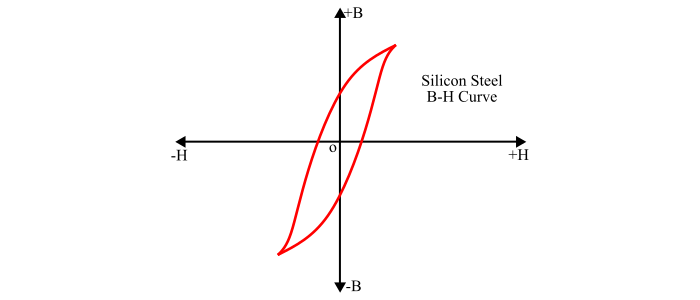
The larger the area of hysteresis loop of a magnetic material, the greater is the hysteresis loss (e.g. hard steel). Therefore, the hard steel is used for making permanent magnets because this material has high retentivity and coercivity.
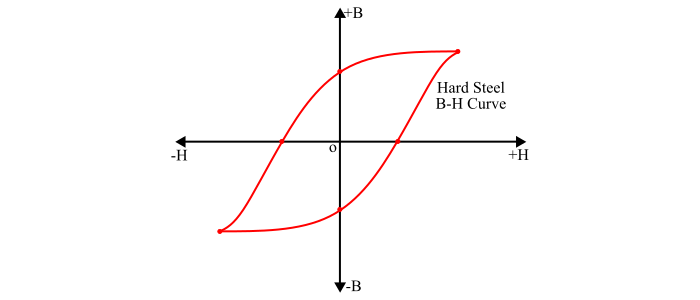
The hysteresis loop for wrought iron has fairly good residual magnetism and coercivity. Therefore, it is used for making cores of electromagnets.
762 Views
