Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Lowest Common Ancestor of Deepest Leaves in Python\n
Suppose we have a rooted binary tree, we have to return the lowest common ancestor of its deepest leaves. We have to keep in mind that −
The node of a binary tree is a leaf node if and only if it has no children
The depth of the root of the tree is 0, and when the depth of a node is d, the depth of each of its children is d+1.
The lowest common ancestor of a set S of nodes in the node A with the largest depth such that every node in S is in the subtree with root A.
If the input is [1,2,3,4,5],
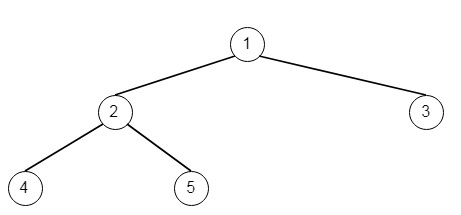
then the output will be [2,4,5]
To solve this, we will follow these steps −
Define a method called solve(), this will take node, this will work as follows −
if node is not present, then return a list with [0, None]
if left and right subtrees are empty of node, then return a list with [1, None]
d1, l := solve(left of node), d2, r := solve(right of node)
if d1 > d2 , then return a list with values [d1 + 1, l]
otherwise when d2 > d1, then return a list with values [d2 + 1, r]
return a list with values [d1 + 1, node]
In the main method, we will perform −
list := solve(root)
return list[1]
Example(Python)
Let us see the following implementation to get a better understanding −
class TreeNode: def __init__(self, data, left = None, right = None): self.data = data self.left = left self.right = right def insert(temp,data): que = [] que.append(temp) while (len(que)): temp = que[0] que.pop(0) if (not temp.left): if data is not None: temp.left = TreeNode(data) else: temp.left = TreeNode(0) break else: que.append(temp.left) if (not temp.right): if data is not None: temp.right = TreeNode(data) else: temp.right = TreeNode(0) break else: que.append(temp.right) def make_tree(elements): Tree = TreeNode(elements[0]) for element in elements[1:]: insert(Tree, element) return Tree def print_tree(root): #print using inorder traversal if root is not None: print_tree(root.left) print(root.data, end = ', ') print_tree(root.right) class Solution(object): def lcaDeepestLeaves(self, root): return self.solve(root)[1] def solve(self,node): if not node: return [0,None] if not node.left and not node.right: return [1,node] d1,l = self.solve(node.left) d2,r = self.solve(node.right) if d1>d2: return [d1+1,l] elif d2>d1: return [d2+1,r] return [d1+1,node] ob = Solution() root = make_tree([1,2,3,4,5]) print_tree(ob.lcaDeepestLeaves(root))
Input
[1,2,3,4,5]
Output
4, 2, 5,
105 Views
