Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Inductors in Series (With and Without Mutual Inductance)
When two inductors are joined end to end i.e. finishing end of one joined to the starting end of the other and same current flows through both the inductors, then the inductors are said to be connected in series.
Inductors in Series with No Mutual Inductance
Consider two inductors of inductance $L_{1}$ and $L_{2}$ connected in series (see the figure). Assume that the mutual inductance between the two coils is zero. Let $L_{T}$ being the total equivalent inductance of the series connected inductors.
Suppose at any instant the current is changing at the rate of di/dt. The total induced emf in the circuit will be equal to the sum of emfs induced in $L_{1}$ and $L_{2}$.
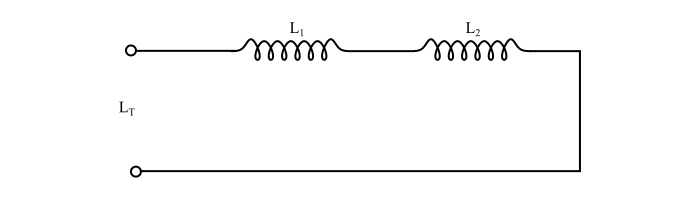
By referring the figure, we have,
$$\mathrm{e=L_{1}\frac{di}{dt}+L_{2}\frac{di}{dt}}$$
$$\mathrm{\Longrightarrow e=(L_{1}+L_{2})\frac{di}{dt}}$$
Also,
$$\mathrm{e=L_{T}\frac{di}{dt}}$$
Therefore,
$$\mathrm{L_{T}=L_{1}+L_{2}}$$
Similarly, for n inductors connected in series, the equivalent inductance will be
$$\mathrm{L_{T}=L_{1}+L_{2}+L_{3}+......+L_{n}}$$
Inductors in Series with Mutual Inductance
Consider two inductors are connected in series. Let
$$\mathrm{L_{1} = Inductance \:of \:the\: first \:inductor}$$
$$\mathrm{L{2} = Inductance\: of\: the \:second\: inductor}$$
M = Mutual inductance of between the inductors
Case 1 − Series-Aiding Connection In this case, the two indictors are connected such that their magnetic fluxes aid each other i.e. being in the same direction. Suppose at any instant, the rate of change of current is di/dt. The total induced emf will be equal to the sum of emfs induced in $L_{1}$ and $L_{2}$ along with the mutually induced emfs.
Referring the figure, we get,
$$\mathrm{e=L_{1}\frac{di}{dt}+L_{2}\frac{di}{dt}+M\frac{di}{dt}+M\frac{di}{dt}}$$
$$\mathrm{\Longrightarrow e=(L_{1}+L_{2}+2M)\frac{di}{dt}}$$
If $L_{T}$ being the total inductance of the circuit, then
$$\mathrm{e=L_{1}\frac{di}{dt}}$$
Therefore,
$$\mathrm{L_{T}=L_{1}+L_{2}+2M}$$
Here, magnetic fluxes are aiding.
Case 2 − Series Opposing Connection In this case, the two inductors are connected such that their magnetic fluxes oppose each other i.e. being in the opposite directions. Suppose at any instant, the rate of change of current is di/dt. The total induced emf in the circuit will be equal to the sum of emfs induced in $L_{1}$ and $L_{2}$ minus the mutually induced emfs.
Referring the figure, we get,
$$\mathrm{e=L_{1}\frac{di}{dt}+L_{2}\frac{di}{dt}-M\frac{di}{dt}-M\frac{di}{dt}}$$
$$\mathrm{\Longrightarrow e=(L_{1}+L_{2}-2M)\frac{di}{dt}}$$
If $L_{T}$ being the inductance of the circuit, then
$$\mathrm{e=L_{1}\frac{di}{dt}}$$
Therefore,
$$\mathrm{L_{T}=L_{1}+L_{2}-2M}$$
Here, the magnetic fluxes are subtractive.
2K+ Views
