How to Perform a Chi-Square Goodness of Fit Test in Python

Introduction

Data Scientists often use statistical methods for hypothesis testing to gain insights from the datasets. While there are multiple statistical methods available, this article will discuss the Chi-Square Goodness of fit test with its implementation in Python. The Chi-Square test validates the observed distribution of categorical variables to the expected distribution. It tells us if the available event values differ from the expected values.

Chi-Square Test

You can perform the Chi-Square test to verify the dataset distribution for observed events. The Chi-Square test makes some assumptions which are as follows −

• Variables are independent.

• Only one categorical feature is present.

• Each variable must contain categories with more than five frequency counts.

• Randomly sampled dataset.

• Every data group must show mutual exclusiveness in frequency counts.

Chi-Square Test Statistic

The Chi-Square test uses the following formula to give statistical output −

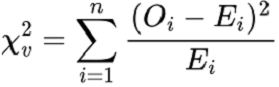
Where

• v denotes the degree of freedom

• O implies the sample observed values

• E stands for the population expected values

• n indicates the variable category counts.

Now let's learn how we can perform the Chi-Square test.

Hypothesis Testing Steps

There are a few steps in performing the Chi-Square test that are as follows −

• At first, you need to create a Null hypothesis, H0, and an Alternate hypothesis, H1.

• Then you need to decide the probability threshold for accepting or rejecting the null hypotheses. The typical value for this threshold is 5%, and the corresponding critical value depends on the distribution.

• Then calculate the Chi-Square statistic using the above formula.

• At last, you need to compare the test statistic value with the critical value. If the test static is greater than the critical value, then we reject the null hypothesis; otherwise, we fail to reject the null hypothesis.

Let us implement the test using the above-mentioned steps −

Here, the null hypothesis is that the variable is distributed in a predetermined way. And the alternate hypothesis is variable is not differently distributed. We will implement the Chi-Square test with two approaches, discussed below −

Implementing Chi-Square with Builtin Function

Syntax

chi_square_test_statistic, p_value = stats.chisquare(
	experience_in_years, Salary)

This function takes two features, applies the chi-square formula to them, and returns the chi-square test statistics and p_value.

Algorithm

• Load the required dependencies like scipy and numpy.

• Pass the features to the chi-square function of scipy.stats on which you want to apply the test statistic.

• Get the test statistic and p_value.

• Accept or Reject the null and alternate hypothesis based on p-value and chi-square statistic.

Example

The process starts with loading all the necessary dependencies.

# importing packages
import scipy.stats as stats
import numpy as np

Let us prepare a demo data where we would have two columns “experience_in_years” and “salary”. For this data, we would be performing Chi-Square test.

# No of years of experience of an employee
# Yearly Salary package in lakhs

experience_in_years= [8, 6, 10, 7, 8, 11, 9]
Salary= [9, 8, 11, 8, 10, 7, 6]

# Chi-Square Goodness of Fit Test
chi_square_test_statistic, p_value = stats.chisquare(
	experience_in_years, Salary)

# chi square test statistic and p value
print('chi_square_test_statistic is : ' +
	str(chi_square_test_statistic))
print('p_value : ' + str(p_value))

# find Chi-Square critical value
print(stats.chi2.ppf(1-0.05, df=6))

Explanation

The above code is the Python implementation of Chi-Square test using in-built function in Scipy library. The chisquare method was imported from stats which returns two values: chi_square_test_statistic, and p-value. This method takes two features and will compare both the variables and apply the abovementioned chi-square formula to calculate the chi-square statistics. Here, we are comparing the relationship between the number of experiences in years and the package per annum (salary).

Output

chi_square_test_statistic is : 5.0127344877344875
p_value : 0.542180861413329
12.591587243743977

As we can see here, the p-value is 0.54 and the critical value is 12.59. The test statistic is less than the critical value hence we can accept the null hypothesis and reject the alternate hypothesis.

Implementing Chi-Square from Scratch

Syntax

chi_square_test_statistic1 = chi_square_test_statistic1 + \
   (np.square(experience_in_years[i]-salary[i]))/salary[i]

Calculate the chi-square value of each sample in the dataset using the abovementioned formula and add them together to get the final score.

Algorithm

• Load the required dependencies like numpy.

• Initialize a variable with value 0 which would store the final value for the statistic.

• Iterate over each sample in the data and calculate the statistics for each sample and add it to the variable that contains the final value for the statistic.

• Once the statistic is calculated, accept or reject the null and alternate hypothesis.

Example

This approach will implement the Chi-Square goodness of fit test using the formula. This method will yield the same results as the above method.

import scipy.stats as stats
import numpy as np

# No of years of experience of an employee
# Yearly Salary package in lakhs 
experience_in_years= [8, 6, 10, 7, 8, 11, 9]
salary= [9, 8, 11, 8, 10, 7, 6]

# determining chi square goodness of fit using formula
chi_square_test_statistic1 = 0
for i in range(len(experience_in_years)):
	chi_square_test_statistic1 = chi_square_test_statistic1 + \
		(np.square(experience_in_years[i]-salary[i]))/salary[i]

print('chi square value determined by formula : ' +
	str(chi_square_test_statistic1))

# find Chi-Square critical value
print(stats.chi2.ppf(1-0.05, df=6))

Explanation

The above code has been implemented in Python to perform Chi-Square test on the same data. In this method, we have implemented the chi-square statistic formula in Python only instead importing the in-built method. The for loop helps iterate through the datasets. Then we implemented the above-mentioned formula with NumPy and added the score with the previous score to get the overall score for the whole dataset. At last, we check the chi-square statistics got using this method.

Output

chi square value determined by formula : 5.0127344877344875
12.591587243743977

As we expected, the results are the same as those we got using the previous method. This result also shows that we should not reject the null hypothesis but we can reject the alternate hypothesis.

Conclusion

We have learned about the Chi-Square Goodness of fit test and how to implement it using Python. Let us summarize the article with a few key takeaways −

• The Chi-Square test verifies the distribution of the observed categorical variable with the expected variable distribution.

• The Chi-Square test makes some assumptions, including only one categorical variable, independent variables, at least five unique categories, and randomly sampled data.

• We conclude the test results by accepting or rejecting the null hypothesis.

• The threshold value must be lesser than the critical value for accepting the null hypothesis.