Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How to identify if a language is regular or not in TOC?
To identify whether a language is regular or not, is based on Pigeon Hole Principle. This is generally called as the Pumping Lemma.
Pumping lemma for Regular languages
It gives a method for pumping (generating) many substrings from a given string.
In other words, we say it provides means to break a given long input string into several substrings.
It gives the necessary condition(s) to prove a set of strings is not regular.
But the pumping lemma is a contradiction test. This means if any language does not satisfy pumping lemma, then we can say that it is not regular. However, if it satisfies the conditions, then we can say that the language may or may not be regular.
Pumping Lemma is a mathematical proof, which takes more time and also sometimes creates a lot of confusion.
Every finite language is regular, that means if there is a limit to the language then we can say it is regular.
For example, consider the language given below −
L = { a10b20} is regular language whereas,
L = { anbn| n > 0} is not regular.
Suppose, if there is an infinite language, then we will check whether its deterministic finite automata (DFA) can be created or not. If we can’t create, then it will not be a regular language.
String length is in arithmetic progression and also, there should be a pattern in the language otherwise finite automata (FA) cannot be created.
Let’s consider some examples to identify whether the language is regular or not
Every finite set represents a regular language.
Example 1
Let us consider all strings of length 2 over an alphabet {a, b}*
Then the language is as follows and is regular −
L = {aa, ab, ba, bb}.
In the above problem given an expression of all strings of length 2 over {a, b}* which is a non-regular language, but the value is bounded by some constant like length 2. So, we can say that the language is regular. This can be proved by taking contradiction.
Example 2
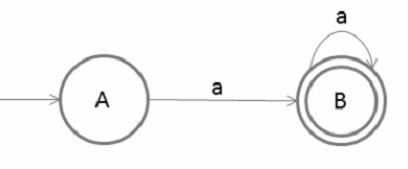
Find out whether the language L = {an | n ≥1} is regular or not.
If we observe the given question clearly there is a pattern in the language and FA can also be generated for the given language. So, we can say the given language is a regular language.
The DFA for the given language is as follows −
4K+ Views
