Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How to find the Fourier Transform of an image using OpenCV Python?
The Discrete Fourier Transform (DFT) and Inverse Discrete Fourier Transform (IDFT) are applied on images to find the frequency domain. To find the Fourier transforms of an image we use the functions cv2.dft() and cv2.idft(). We can apply Fourier Transform to analyze the frequency characteristics of various filters.
Steps
To find Fourier transforms of an input image, one could follow the steps given below −
Import the required libraries. In all below Python examples the required Python libraries are OpenCV, Numpy and Matplotlib. Make sure you have already installed them.
Load the input image as a grayscale image using cv2.imread() method. Also convert the type of gray image to float32.
Find Discrete Fourier Transform on the image using cv2.dft() passing required arguments.
Call np.fft.fftshift() to shift the zero-frequency component to the center of the spectrum.
Apply log transform and visualize the magnitude spectrum.
To visualize the transformed image we apply inverse transforms np.fft.ifftshift() and cv2.idft(). See the second example discussed below.
Let's look at some examples for a clear understanding about the question.
Input Image
We will use this image as an input file in the examples below.
Example
In this program, we find the discrete fourier transform of the input image. We find and plot the magnitude spectrum.
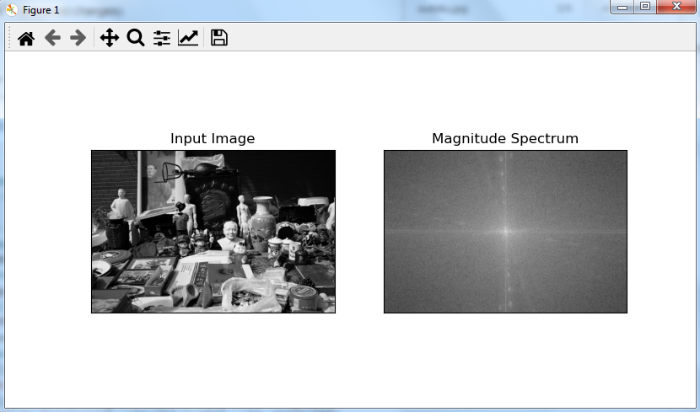
# import required libraries import numpy as np import cv2 from matplotlib import pyplot as plt # read input image img = cv2.imread('film.jpg',0) # find the discrete fourier transform of the image dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT) # shift zero-frequency component to the center of the spectrum dft_shift = np.fft.fftshift(dft) magnitude_spectrum = 20*np.log(cv2.magnitude( dft_shift[:,:,0], dft_shift[:,:,1]) ) # visualize input image and the magnitude spectrum plt.subplot(121),plt.imshow(img, cmap = 'gray') plt.title('Input Image'), plt.xticks([]), plt.yticks([]) plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray') plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([]) plt.show()
Output
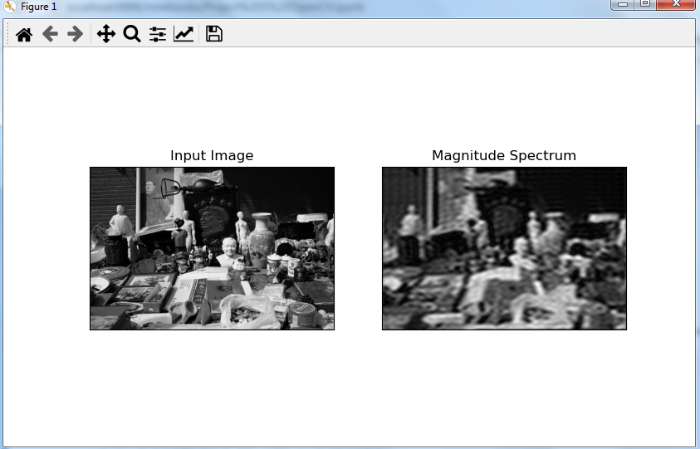
When you run the above Python program, it will produce the following output window −
Example
In this program, we find the discrete fourier transform of the input image. We reconstruct the image using inverse functions such as ifftshift() and idft().
import numpy as np import cv2 from matplotlib import pyplot as plt # read the input image img = cv2.imread('film.jpg',0) # find the discrete fourier transform of the image dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT) # hift zero-frequency component to the center of the spectrum dft_shift = np.fft.fftshift(dft) rows, cols = img.shape crow,ccol = rows//2 , cols//2 mask = np.zeros((rows,cols,2),np.uint8) mask[crow-30:crow+30, ccol-30:ccol+30] = 1 # apply mask and inverse DFT fshift = dft_shift*mask f_ishift = np.fft.ifftshift(fshift) img_back = cv2.idft(f_ishift) img_back = cv2.magnitude(img_back[:,:,0],img_back[:,:,1]) # visualize the images plt.subplot(121),plt.imshow(img, cmap = 'gray') plt.title('Input Image'), plt.xticks([]), plt.yticks([]) plt.subplot(122),plt.imshow(img_back, cmap = 'gray') plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([]) plt.show()
Output
When you run the above Python program, it will produce the following output window −
3K+ Views
